library(tidyverse)
library(psych)
fa.pc.varimax <- car_sales %>% select(engine_s:mpg) %>%
principal(nfactors = 2,
rotate = "varimax")
fa.pc.varimax
Principal Components Analysis
Call: principal(r = ., nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
RC1 RC2 h2 u2 com
engine_s 0.88 0.32 0.87 0.13 1.3
horsepow 0.89 0.09 0.80 0.20 1.0
wheelbas 0.19 0.94 0.91 0.09 1.1
width 0.52 0.69 0.75 0.25 1.9
length 0.23 0.89 0.84 0.16 1.1
curb_wgt 0.72 0.58 0.85 0.15 1.9
fuel_cap 0.64 0.59 0.76 0.24 2.0
mpg -0.80 -0.37 0.78 0.22 1.4
RC1 RC2
SS loadings 3.49 3.06
Proportion Var 0.44 0.38
Cumulative Var 0.44 0.82
Proportion Explained 0.53 0.47
Cumulative Proportion 0.53 1.00
Mean item complexity = 1.5
Test of the hypothesis that 2 components are sufficient.
The root mean square of the residuals (RMSR) is 0.07
with the empirical chi square 38.95 with prob < 2e-04
Fit based upon off diagonal values = 0.99
print(fa.pc.varimax$loadings, digits = 3, cutoff = 0.5,sort = T)
Loadings:
RC1 RC2
engine_s 0.876
horsepow 0.888
curb_wgt 0.722 0.577
fuel_cap 0.644 0.586
mpg -0.803
wheelbas 0.935
width 0.517 0.693
length 0.888
RC1 RC2
SS loadings 3.493 3.063
Proportion Var 0.437 0.383
Cumulative Var 0.437 0.819
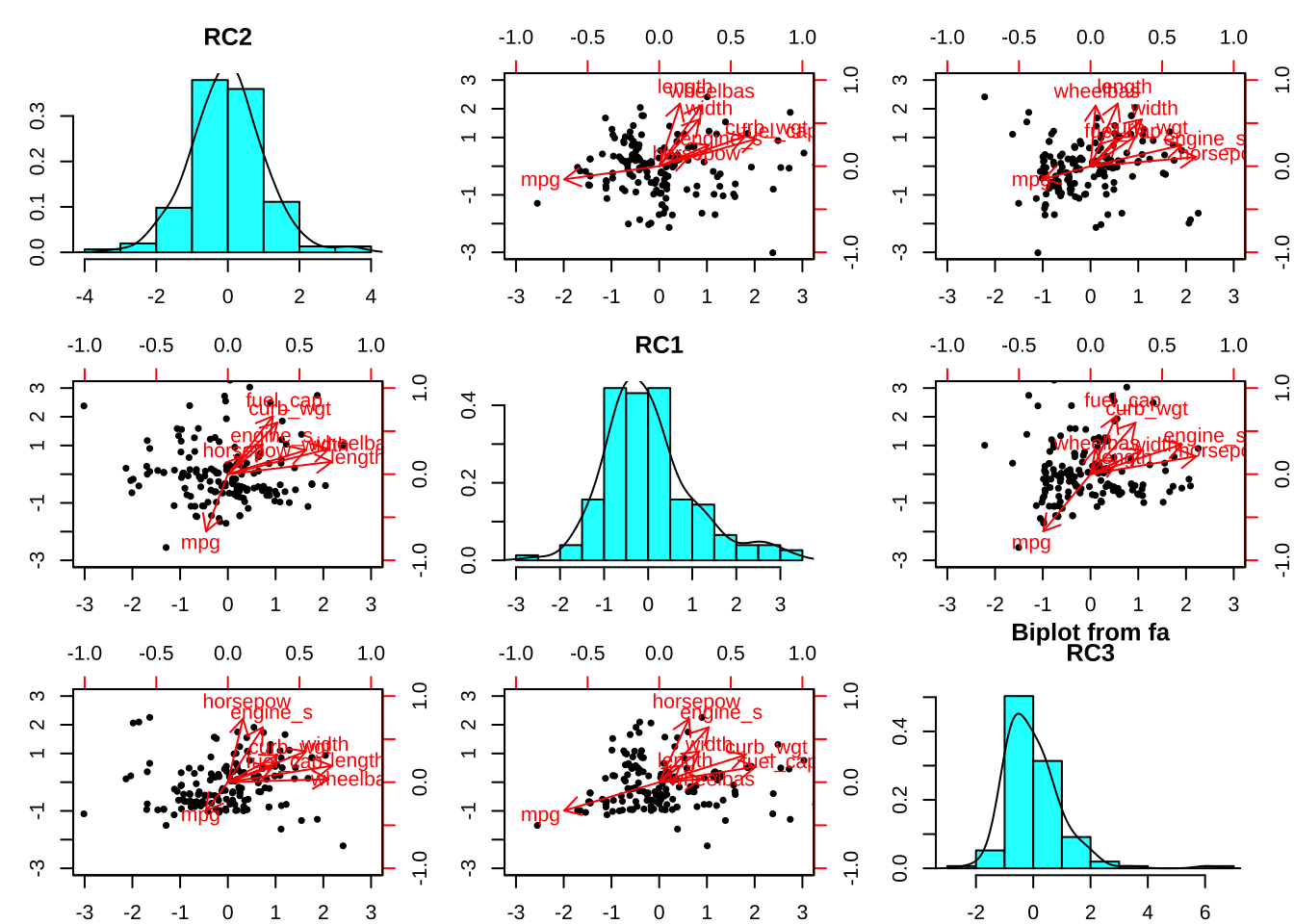
fa.pc.varimax <- car_sales %>% select(engine_s:mpg) %>%
principal(nfactors = 3,
rotate = "varimax")
fa.pc.varimax
Principal Components Analysis
Call: principal(r = ., nfactors = 3, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
RC2 RC1 RC3 h2 u2 com
engine_s 0.31 0.43 0.80 0.92 0.084 1.9
horsepow 0.13 0.26 0.92 0.93 0.066 1.2
wheelbas 0.88 0.37 0.04 0.91 0.090 1.3
width 0.68 0.35 0.45 0.78 0.216 2.3
length 0.91 0.18 0.24 0.91 0.085 1.2
curb_wgt 0.43 0.75 0.39 0.90 0.099 2.2
fuel_cap 0.39 0.84 0.22 0.91 0.085 1.6
mpg -0.19 -0.83 -0.41 0.89 0.107 1.6
RC2 RC1 RC3
SS loadings 2.55 2.50 2.12
Proportion Var 0.32 0.31 0.26
Cumulative Var 0.32 0.63 0.90
Proportion Explained 0.36 0.35 0.30
Cumulative Proportion 0.36 0.70 1.00
Mean item complexity = 1.7
Test of the hypothesis that 3 components are sufficient.
The root mean square of the residuals (RMSR) is 0.03
with the empirical chi square 8.66 with prob < 0.28
Fit based upon off diagonal values = 1
print(fa.pc.varimax$loadings, digits = 3, cutoff = 0.5,sort = T)
Loadings:
RC2 RC1 RC3
wheelbas 0.879
width 0.680
length 0.908
curb_wgt 0.748
fuel_cap 0.842
mpg -0.829
engine_s 0.797
horsepow 0.922
RC2 RC1 RC3
SS loadings 2.550 2.500 2.119
Proportion Var 0.319 0.312 0.265
Cumulative Var 0.319 0.631 0.896
library(tidyverse)
data <- cbind(car_sales, fa.pc.varimax$scores)
data <- data %>% mutate(suv = if_else(type == 1, 1,0))
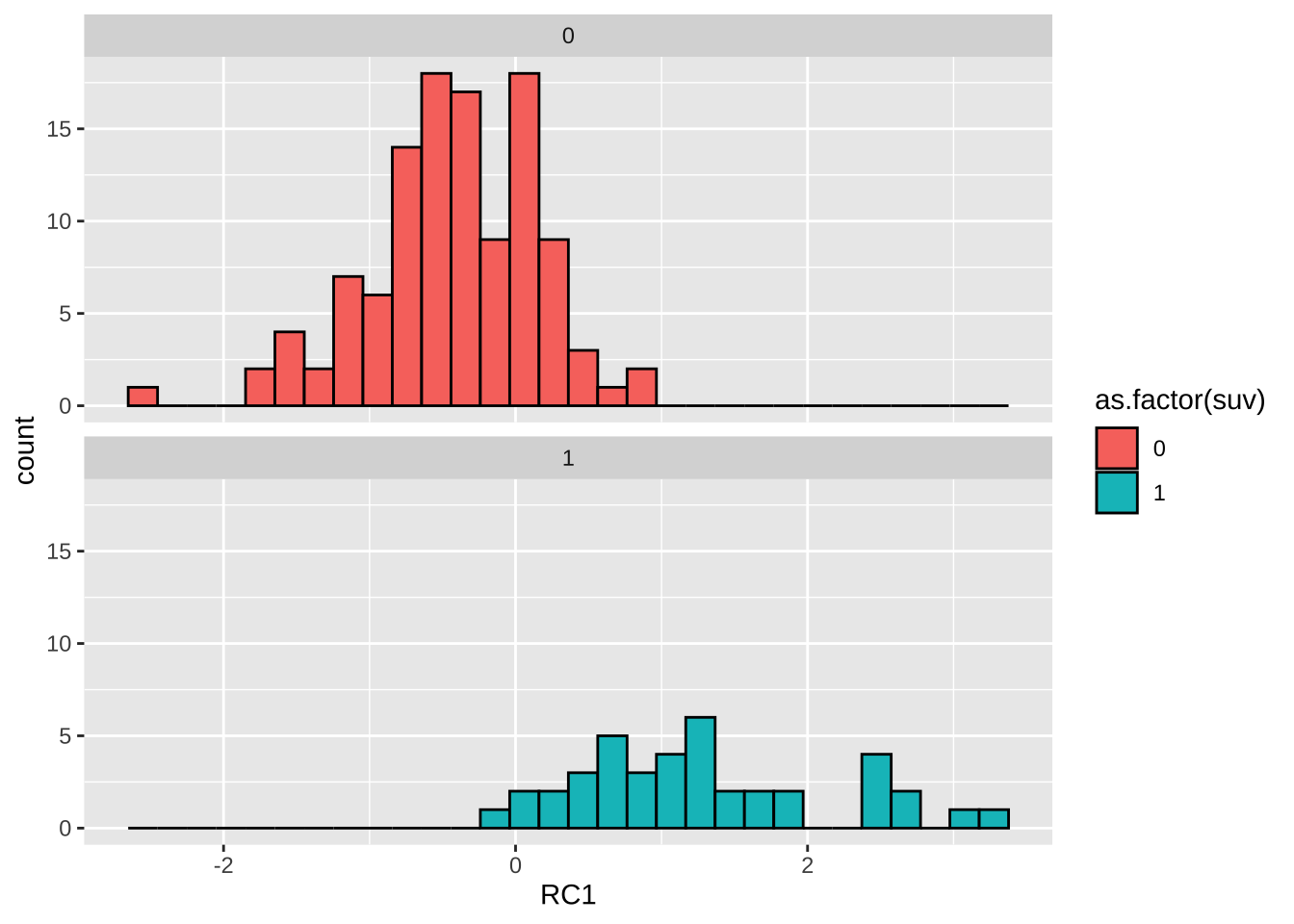
# RC1,其值越大,代表车重大、油箱容积大、耗油越高(SUV)
data %>% ggplot(aes(RC1, fill = as.factor(suv)))+
geom_histogram(col = 1)+
facet_wrap(~ suv,ncol = 1)
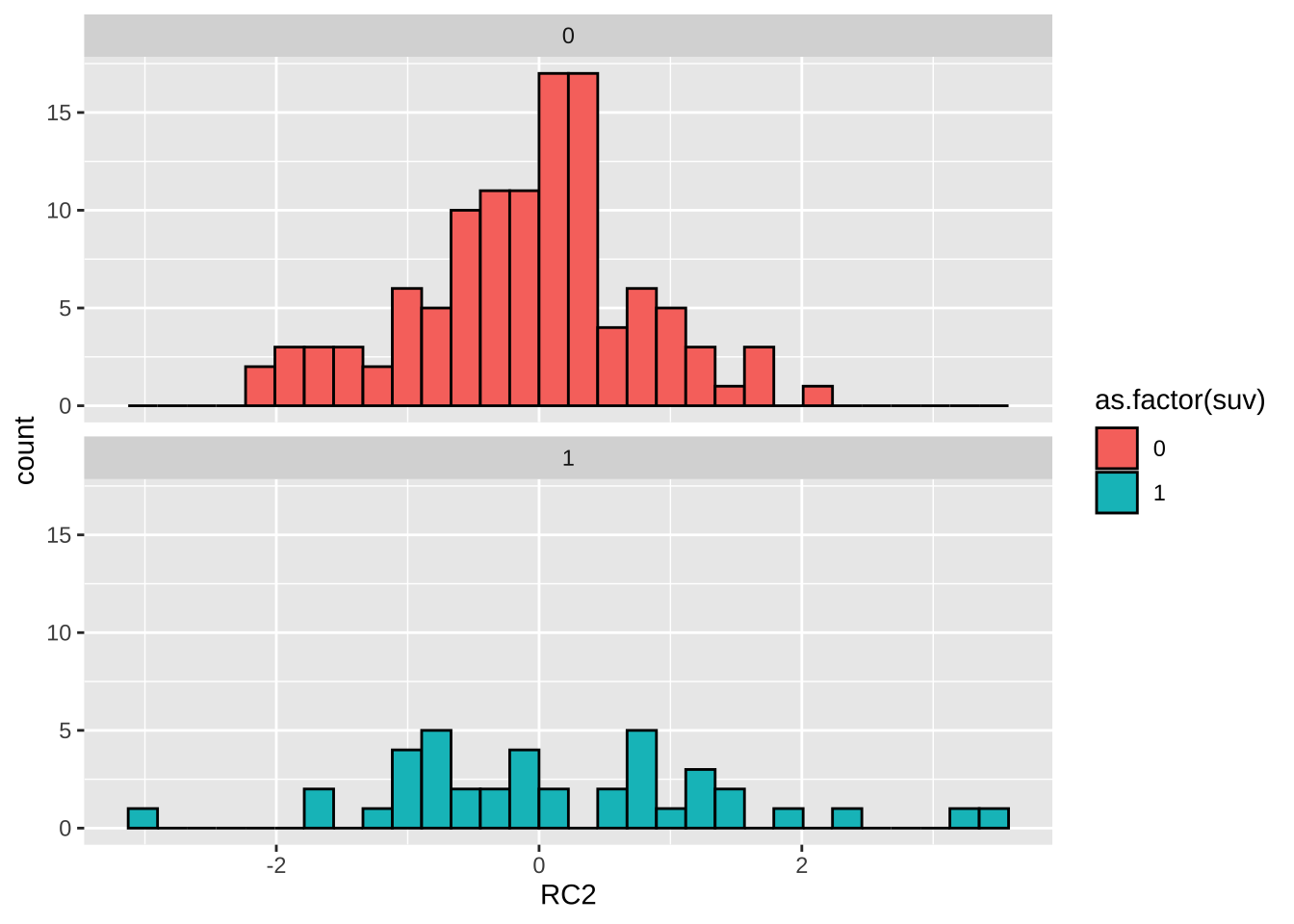
# RC2,其值越大,代表车子轮距、车宽、车长大
data %>% ggplot(aes(RC2, fill = as.factor(suv)))+
geom_histogram(col = 1)+
facet_wrap(~ suv,ncol = 1)
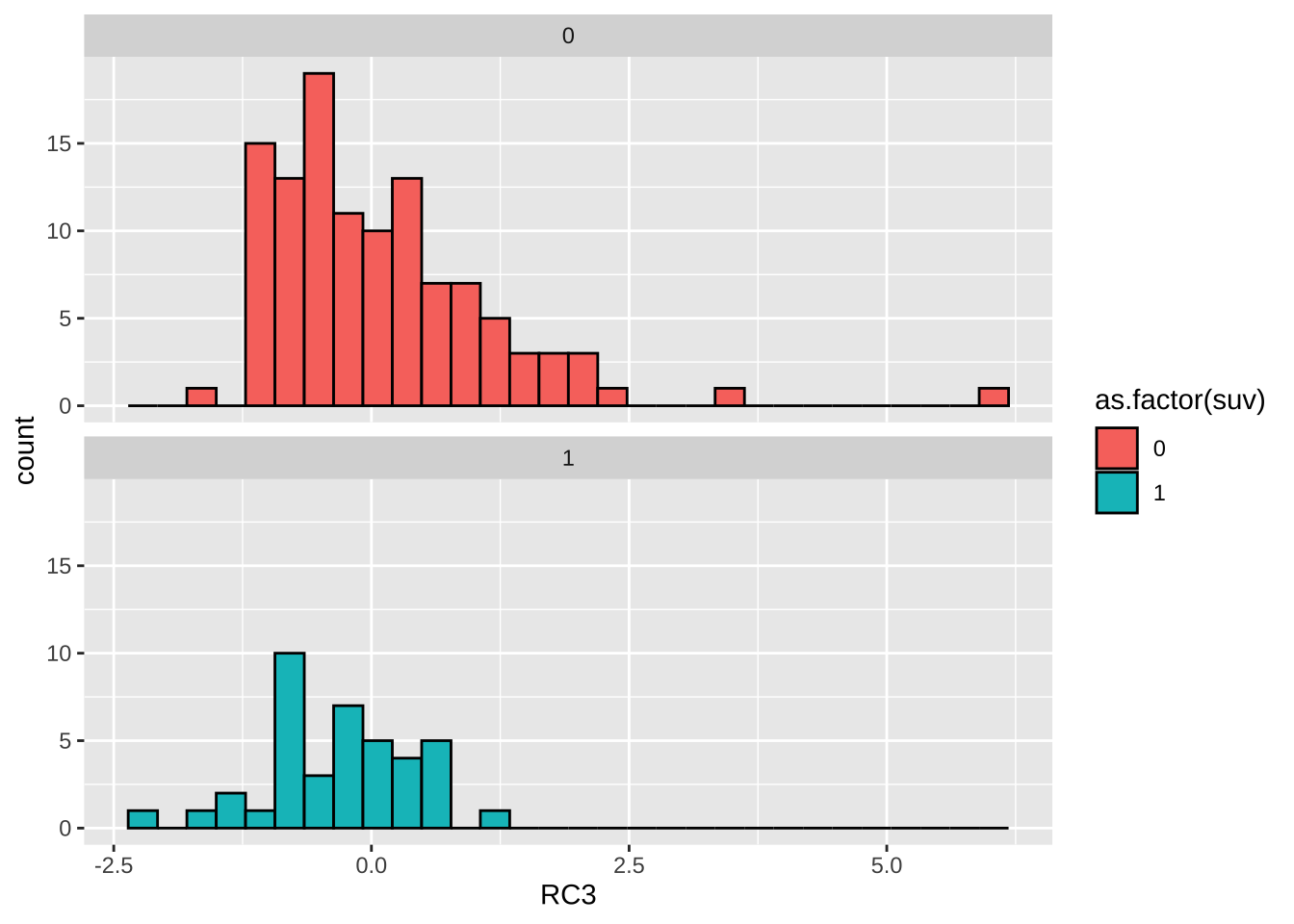
# RC3,动力性能
data %>% ggplot(aes(RC3, fill = as.factor(suv)))+
geom_histogram(col = 1)+
facet_wrap(~ suv,ncol = 1)
eq1 <- lm(price ~ RC1 +RC2 +RC3, data)
summary(eq1)
Call:
lm(formula = price ~ RC1 + RC2 + RC3, data = data)
Residuals:
Min 1Q Median 3Q Max
-21.468 -5.049 -0.936 2.972 36.978
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 27.4646 0.7014 39.156 < 2e-16 ***
RC1 4.3130 0.6999 6.162 6.47e-09 ***
RC2 -1.0709 0.7001 -1.530 0.128
RC3 10.6574 0.7036 15.148 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.643 on 148 degrees of freedom
(5 observations deleted due to missingness)
Multiple R-squared: 0.6479, Adjusted R-squared: 0.6407
F-statistic: 90.76 on 3 and 148 DF, p-value: < 2.2e-16
eq2 <- lm(resale ~ RC1 +RC2 +RC3, data)
summary(eq2)
Call:
lm(formula = resale ~ RC1 + RC2 + RC3, data = data)
Residuals:
Min 1Q Median 3Q Max
-14.680 -4.848 -1.442 2.978 30.519
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.5900 0.7066 26.310 < 2e-16 ***
RC1 3.0571 0.7242 4.222 4.9e-05 ***
RC2 -2.1020 0.6729 -3.124 0.00227 **
RC3 7.5295 0.6661 11.303 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.639 on 114 degrees of freedom
(39 observations deleted due to missingness)
Multiple R-squared: 0.5742, Adjusted R-squared: 0.563
F-statistic: 51.25 on 3 and 114 DF, p-value: < 2.2e-16
eq3 <- lm(sales ~ RC1 +RC2 +RC3, data)
summary(eq3)
Call:
lm(formula = sales ~ RC1 + RC2 + RC3, data = data)
Residuals:
Min 1Q Median 3Q Max
-88.46 -35.92 -18.67 20.10 397.87
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 53.30585 5.08555 10.482 < 2e-16 ***
RC1 0.05693 5.08494 0.011 0.99108
RC2 25.16954 5.09264 4.942 2.05e-06 ***
RC3 -14.56111 5.11090 -2.849 0.00501 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 62.88 on 149 degrees of freedom
(4 observations deleted due to missingness)
Multiple R-squared: 0.1808, Adjusted R-squared: 0.1643
F-statistic: 10.96 on 3 and 149 DF, p-value: 1.508e-06
 点击下载数据文件: car_sales.xlsx
点击下载数据文件: car_sales.xlsx