第6章

第6章统计量及其抽样分布

第1题至第6题

在同一个坐标系下，绘制N(0,1)、N(1, 4)、N(-2, 0.25)的概率密度曲线。

在同一个坐标系下，绘制N(0,1)、t(5)、t(10)、t(30)的概率密度曲线。

在同一个坐标系下，绘制\(\chi^2(5)\)、\(\chi^2(10)\)、\(\chi^2(30)\)的概率密度曲线。

在同一个坐标系下，绘制F(2,5)、F(5,10)、F(30,50)的概率密度曲线。

利用Excel生成如下分布的随机数，并绘制直方图。提交直方图的图片。

2.1 生成服从自由度为5的卡方分布的500个随机数，绘制其直方图。

2.2 生成服从自由度为5的t分布的500个随机数，绘制其直方图。

2.3 生成服从自由度为30的卡方分布的500个随机数，绘制其直方图。

2.4 生成服从F(5, 30)的500个随机数，绘制其直方图。

\(Z_{0.05} ; Z_{0.15} ; Z_{0.90}\)
\(Z_{\frac{0.01}{2}} ; Z_{\frac{0.05}{2}} ; Z_{\frac{0.10}{2}}\)
\(X \sim N(0,1), P(X>2.5)=\) ? \(P(X<-2)=\) ? \(P(|X|>1.8)=\) ?
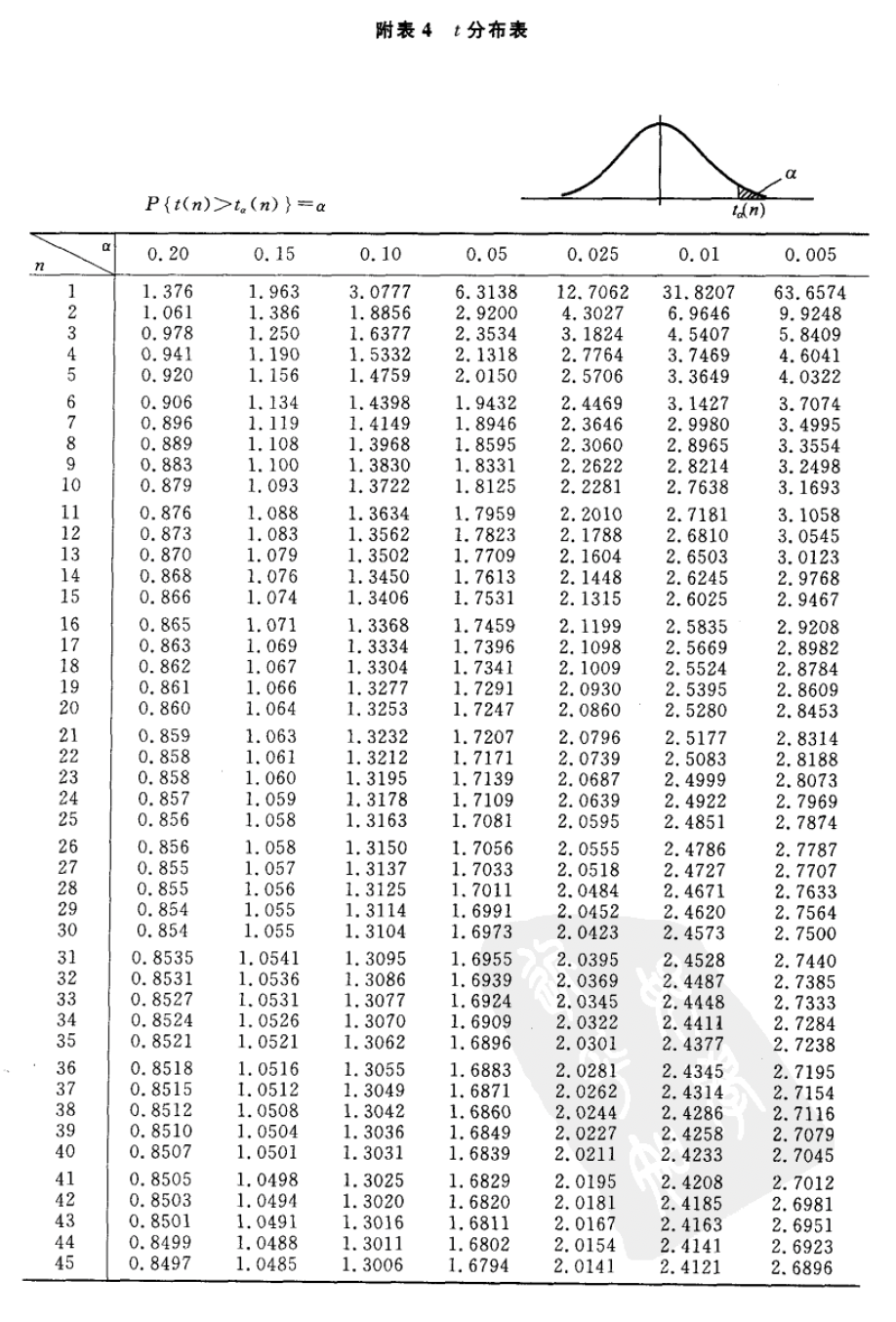
\(t_{0.05}(8) ; t_{\frac{0.05}{2}}(8) ; t_{0.95}(8)\)
\(t_{0.05}(50) ; t_{\frac{0.05}{2}}(50) ; t_{0.95}(50)\)
\(X \sim t(8), P(X>2)=\) ? \(P(X<-1.8)=\) ? \(P(|X|>2)=\) ?
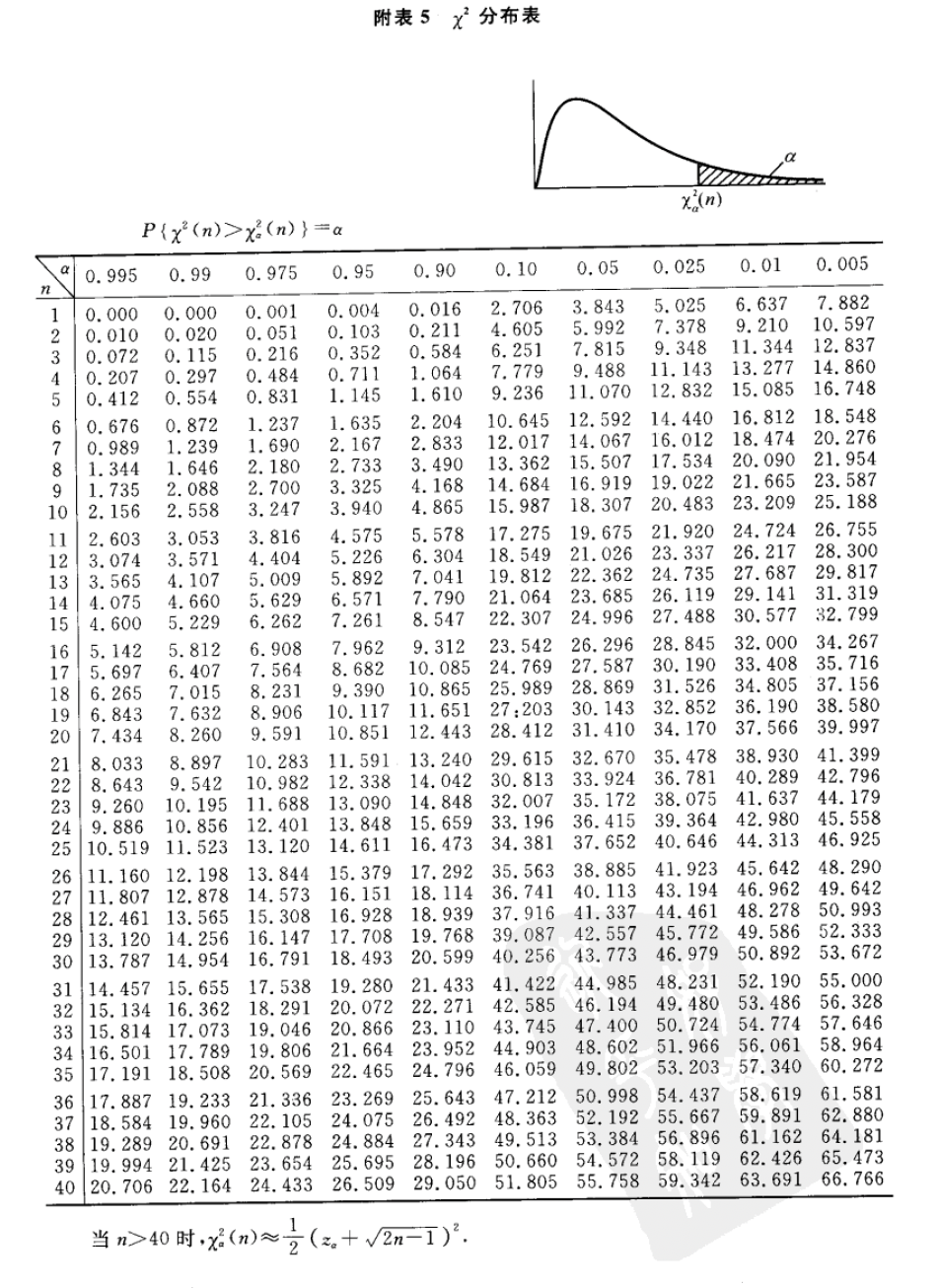
\(\chi_{0.05}^2(5) ; \chi_{0.95}^2(5) ; \chi_{0.05}^2(15) ; \quad \chi_{0.95}^2(15)\)
\(X \sim \chi^2(5), P(X>9)=\) ? ; \(P(X<1)=\) ?
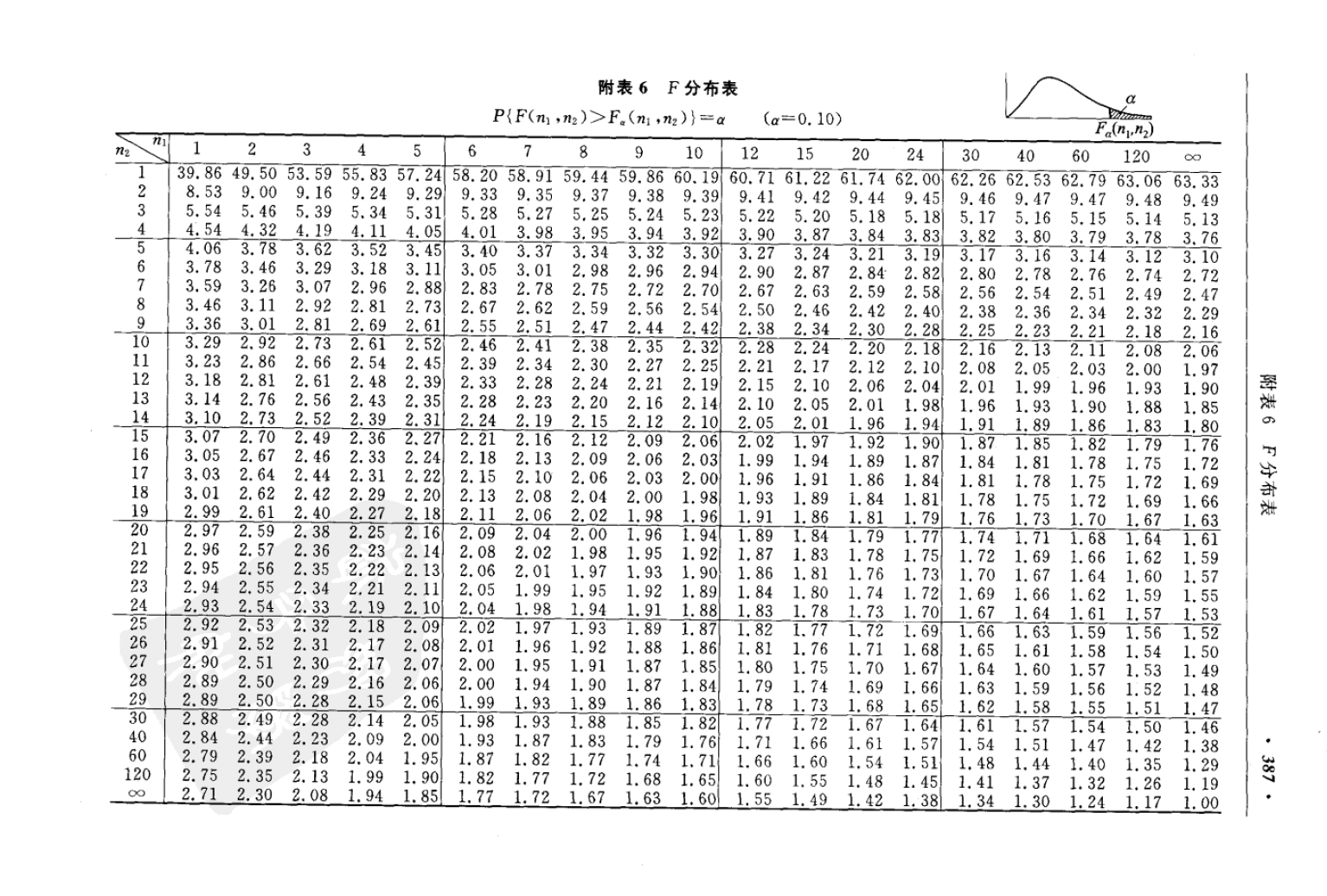
\(F_{0.05}(5,10) ; F_{0.95}(5,10)\);
\(F_{0.05}(10,30) ; F_{0.95}(10,30)\);
\(X \sim F(5,10), P(X>3)=\) ?; \(P(X<1)=\) ?

4.1 生成500个服从正态分布N(100,10^2)的随机数。将这500个数视作总体，从中随机抽取容量为4的样本，重复抽样100次，绘制100个样本的样本均值的直方图。

4.2 生成500个服从正态分布N(100,10^2)的随机数。将这500个数视作总体，从中随机抽取容量为36的样本，复抽样100次，绘制100个样本的样本均值的直方图。

4.3 比较4.1和4.2中的两幅直方图，概括两幅直方图的特征。

5.1 生成1000个服从泊松分布Poisson(5)的随机数。将这1000个数视作总体，从中随机抽取容量为4的样本，重复抽样100次，绘制100个样本的样本均值的直方图。

5.2 生成1000个服从泊松分布Poisson(5)的随机数。将这1000个数视作总体，从中随机抽取容量为36的样本，重复抽样100次，绘制100个样本的样本均值的直方图。

5.3 比较5.1和5.2中的两幅直方图，概括两幅直方图的特征。

6.1 利用Excel绘制标准正态分布表。

6.2 利用Excel绘制t分布表。

6.3 利用Excel绘制卡方分布表。

6.4 利用Excel绘制F分布表。

题目

数据文件：house.xlsx (QQ群文件)

将数据文件中的变量总价万、面积平方米的观测值四舍五入取整。
创建新变量每平方米单价(万/平方米)，保留1位小数。
根据变量区域，将“广州番禺区”记录为“番禺”，将“广州天河区”记录为“天河”，保存到新变量行政区域。
绘制变量“朝向”的频数分布表，将朝向分为东、南、西、北四类，保存到新变量“主朝向”。
根据变量建筑年份，创建新变量“楼龄”。
根据变量“总楼层”，创建新变量“住宅高度”。将楼层为1-6层的，记为“低层”；将楼层为7-11层的记录为小高层；将楼层为12-29层的，记为“高层”；将楼层为30层以上的，记为“超高层”。
选取两个定性变量，绘制簇状条形图。
选取两个定性变量，绘制堆积条形图。
选取两个定性变量，一个定量变量，用条形图反映各个组别的定量变量的均值的大小。
选取一个定性变量，一个定量变量，绘制分组直方图。
选取一个定性变量，两个定量变量，绘制分组散点图。
选取一个定性变量，将样本数据分组，报告各个组别的所有的定量变量的均值、中位数、标准差、最小值和最大值。