EViews 分位数回归模型
估计、检验与可视化
2024-07-01
大纲
1 分位数回归模型简介
2 案例
3 分位数回归模型的估计
4 分位数回归模型的诊断
5 分位数回归模型的可视化
6 分位数回归的EViews代码
7 EViews优势和使用经验
1 分位数回归模型:模型设定
- 分位数回归将被解释变量的条件分位数表示为解释变量的线性函数。
\[ Q_q\left(y_i \mid x_i\right)=x_i^{\prime} \beta_q \]
1 分位数回归模型:估计思想
- 最小化
\[ Q\left(\beta_q\right)=\sum_{i: y_i \geq x_i^{\prime} \beta}^n q\left|y_i-x_i^{\prime} \beta_q\right|+\sum_{i: y_i<x_i^{\prime} \beta}^n(1-q)\left|y_i-x_i^{\prime} \beta_q\right| \]
0<q<1
当q取不同的值时,估计出相应的\(β_q\)。
利用线性规划求解出令\(Q\left(\beta_q\right)\)取到最小值的\(β_q\)
1 分位数回归模型:估计思想
当q等于0.5时:
\[ Q\left(\beta_{0.5}\right)=\sum_i^n\left|y_i-x_i^{\prime} \beta_{0.5}\right| \]
实际上就是所有观测点的残差的绝对值之和。
q等于0.5的分位数回归也称作中位数回归,其估计方法称作最小绝对离差法(Least Absolute-Deviation, 简称LAD)。
1 分位数回归模型:系数含义
\[ \frac{\partial Q_q(y \mid x)}{\partial x_j}=\beta_{q j} \]
\(β_{qj}\)的含义是:当其他变量保持不变,\(x_j\)变化一单位,平均而言,被解释变量的第\(100*q\)个百分位数将变化\(β_{qj}\)单位。
1 分位数回归模型:优势
克服了最小二乘回归模型中潜在的异方差问题
不受样本中异常值的影响,得到稳健的估计结果
能够更加细致地描述变量之间的关系。
1 分位数回归模型:优势
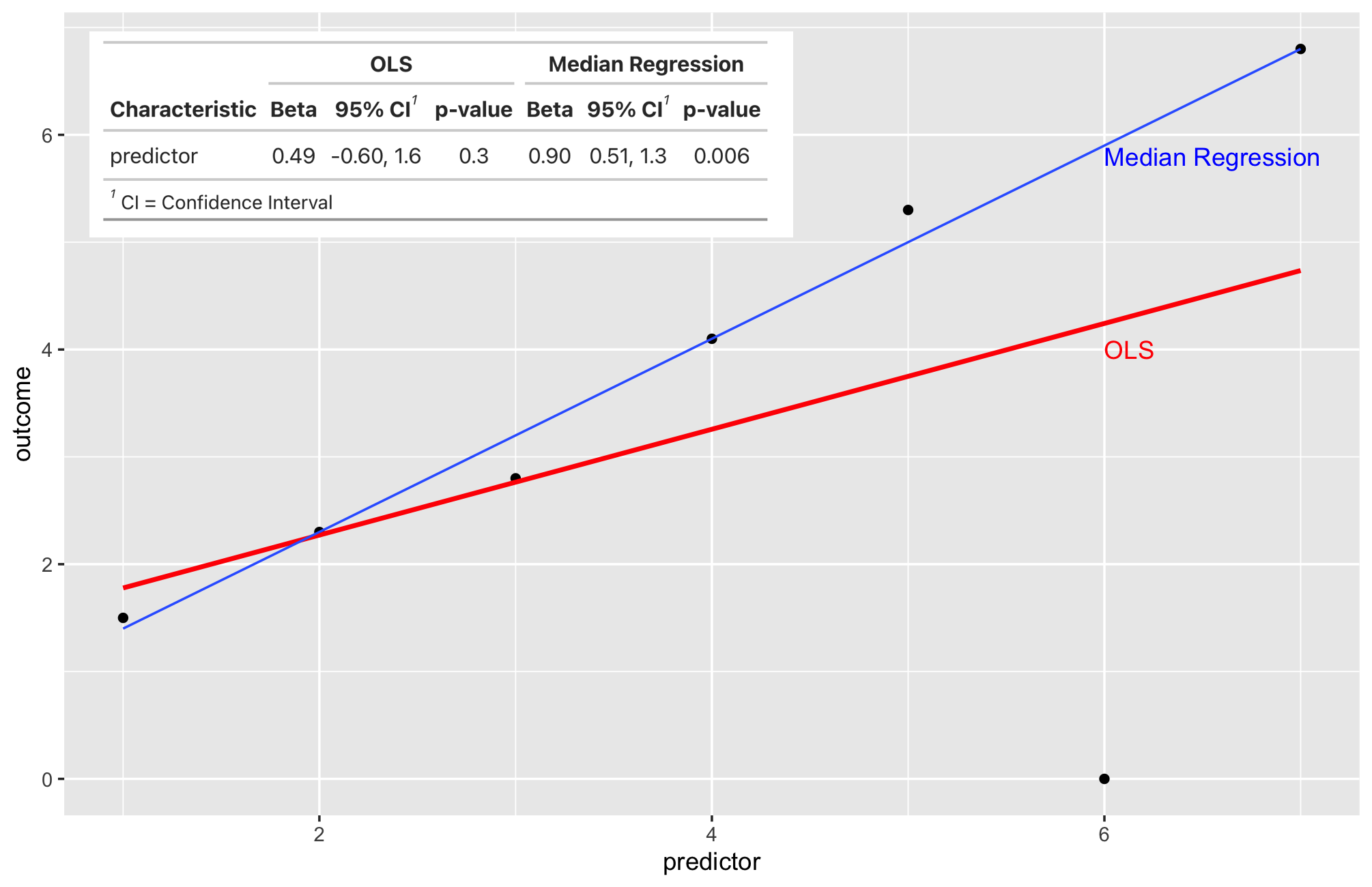
1 分位数回归模型:优势
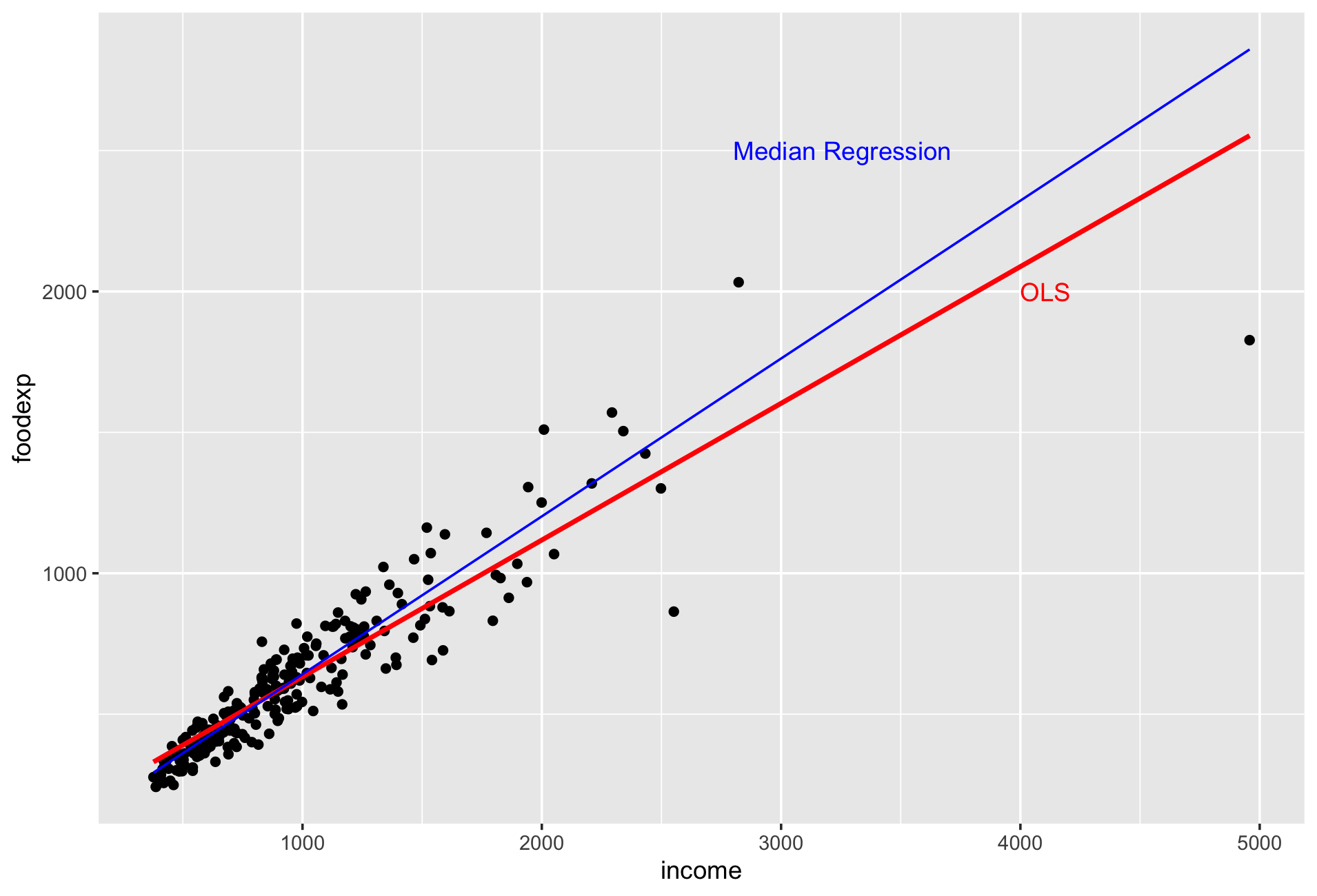
1 分位数回归模型:适用场景
容量很大的样本数据,才适宜探究被解释变量的条件分布与解释变量的关系特征。
若样本容量太小,给定的解释变量和被解释变量的变异程度不够,无法探究其分位数与解释变量的关系。
2 案例: 数据
数据来源:美国医疗费用支出跟踪调查(Medical Expenditure Panel Survey,简称MEPS)
样本数据:从MEPS数据库中提取2955个人的数据

2 案例: 研究目标
建立分位数回归模型,研究个人医疗支出的条件分布与年龄、患有慢性病的个数、是否购买补充医疗保险、性别、人种的关系。
比较分位数回归估计结果与普通最小二乘估计结果。
比较医疗支出高低不同的组别,个人年龄、患有慢性病的个人、是否购买补充医疗保险、性别、人种对医疗支出影响效应的差异。
3 分位数回归模型的估计:模型设定
\[ \begin{aligned} & Q_q\left(totexp_i \mid age_i, totchr_i, suppins_i, female_i, white_i\right) \\ &= \beta_{q0}+\beta_{q1}age_i+\beta_{q2}otchr_i+\beta_{q3}suppins_i \\ & \space \space \space + \beta_{q4}female_i+\beta_{q5}white_i \end{aligned} \]
3 分位数回归模型的估计:Equation Estimation
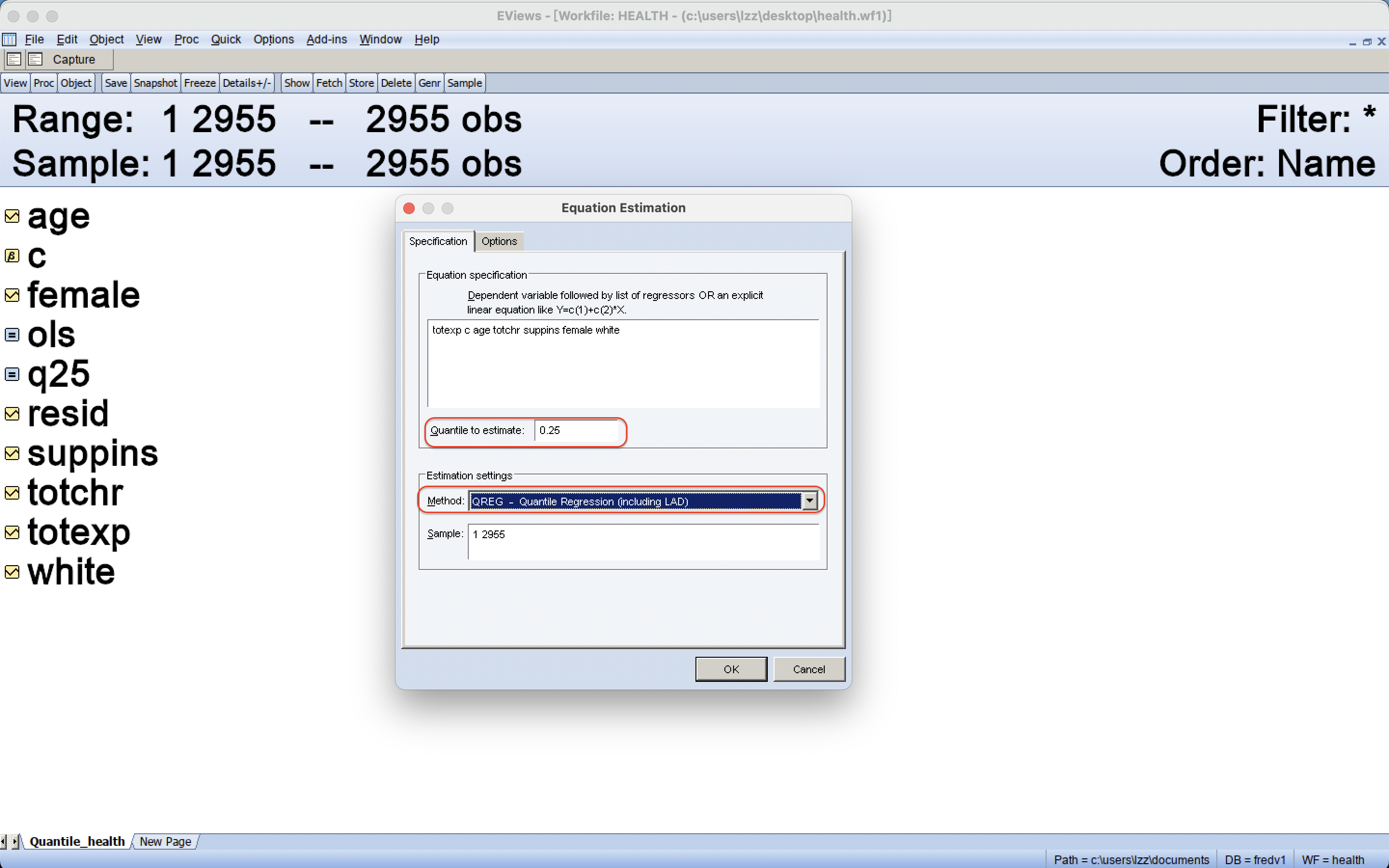
3 分位数回归模型的估计:估计结果
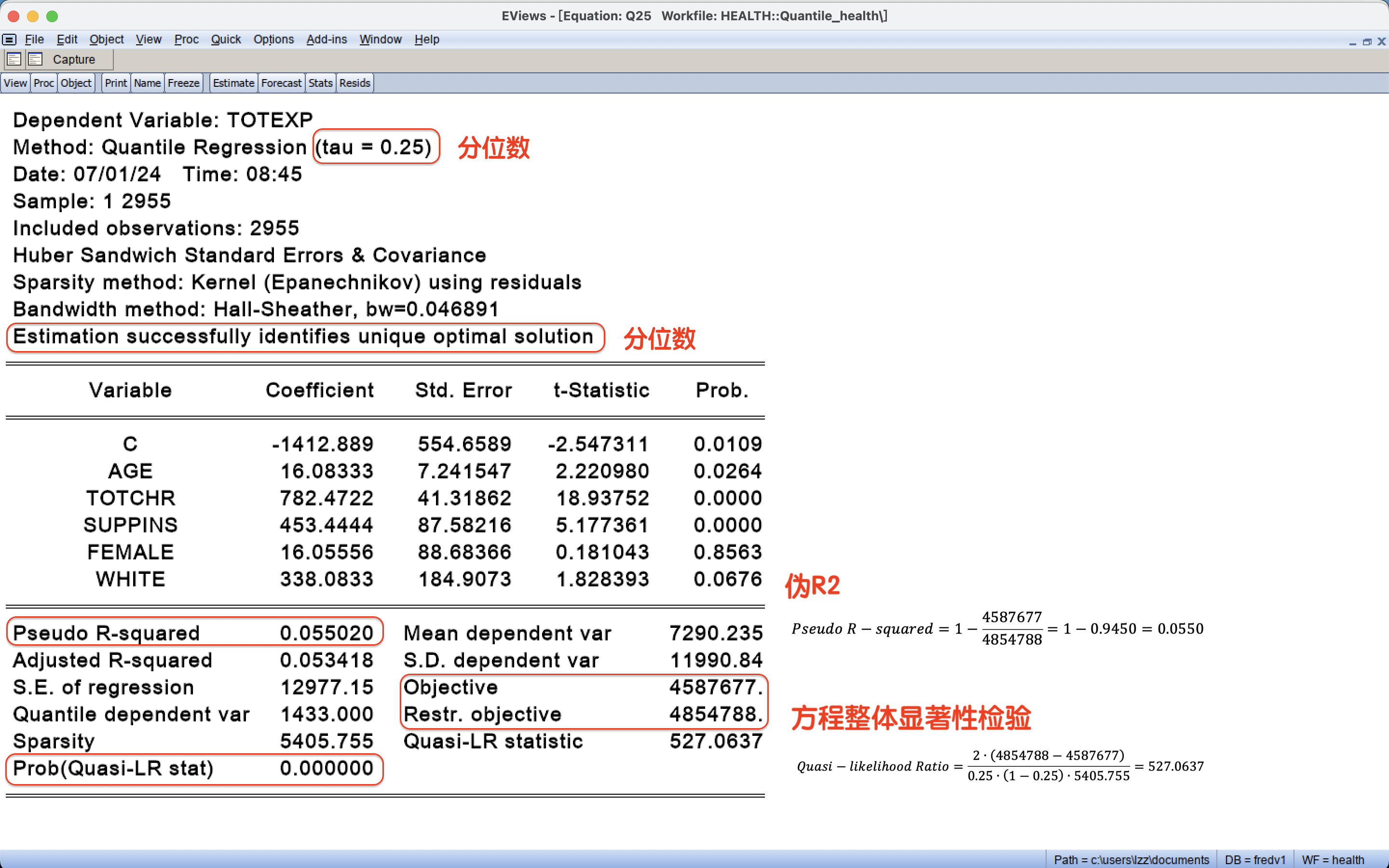
3 分位数回归模型的估计:与OLS对比
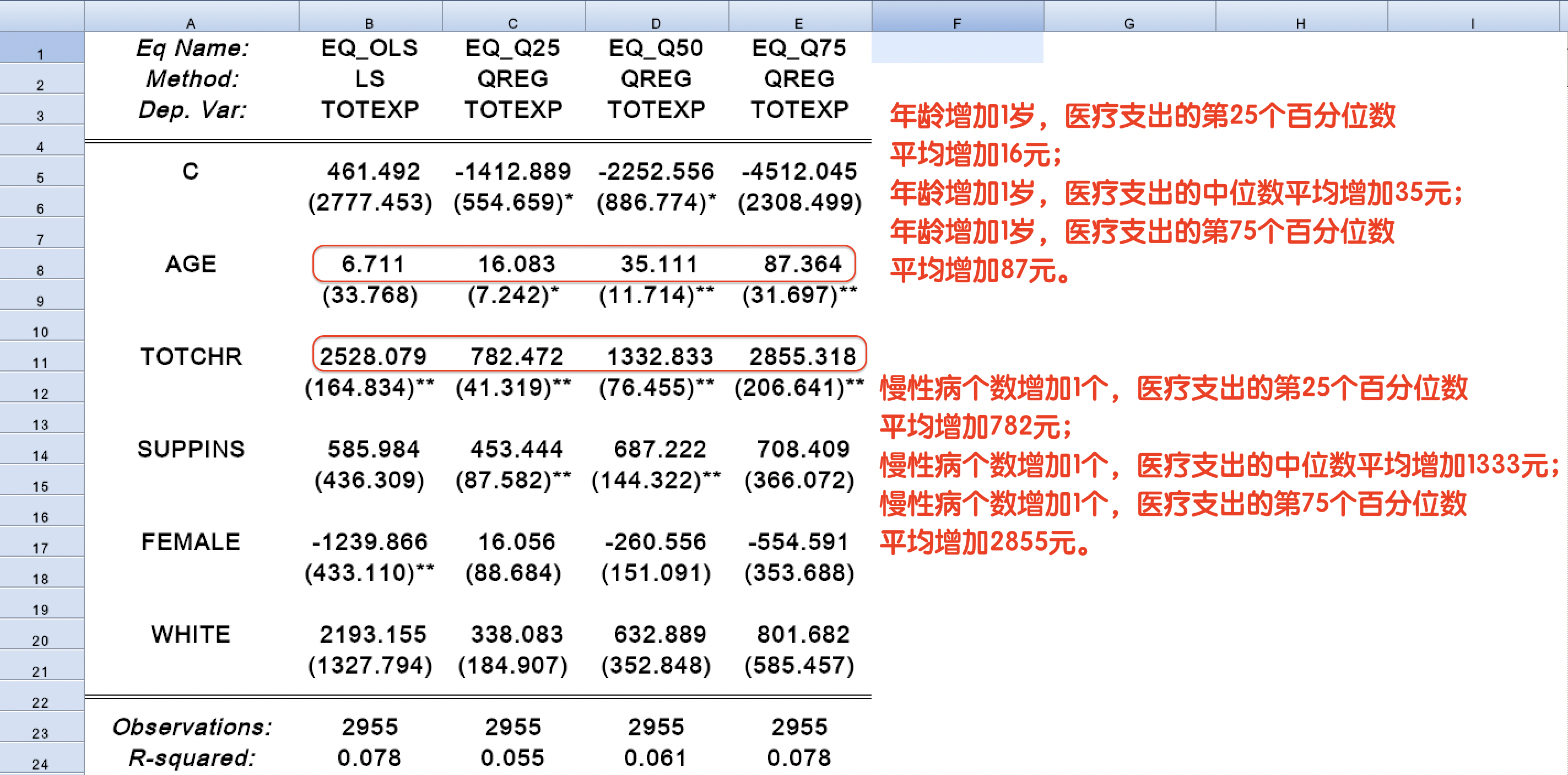
3 分位数回归模型的估计
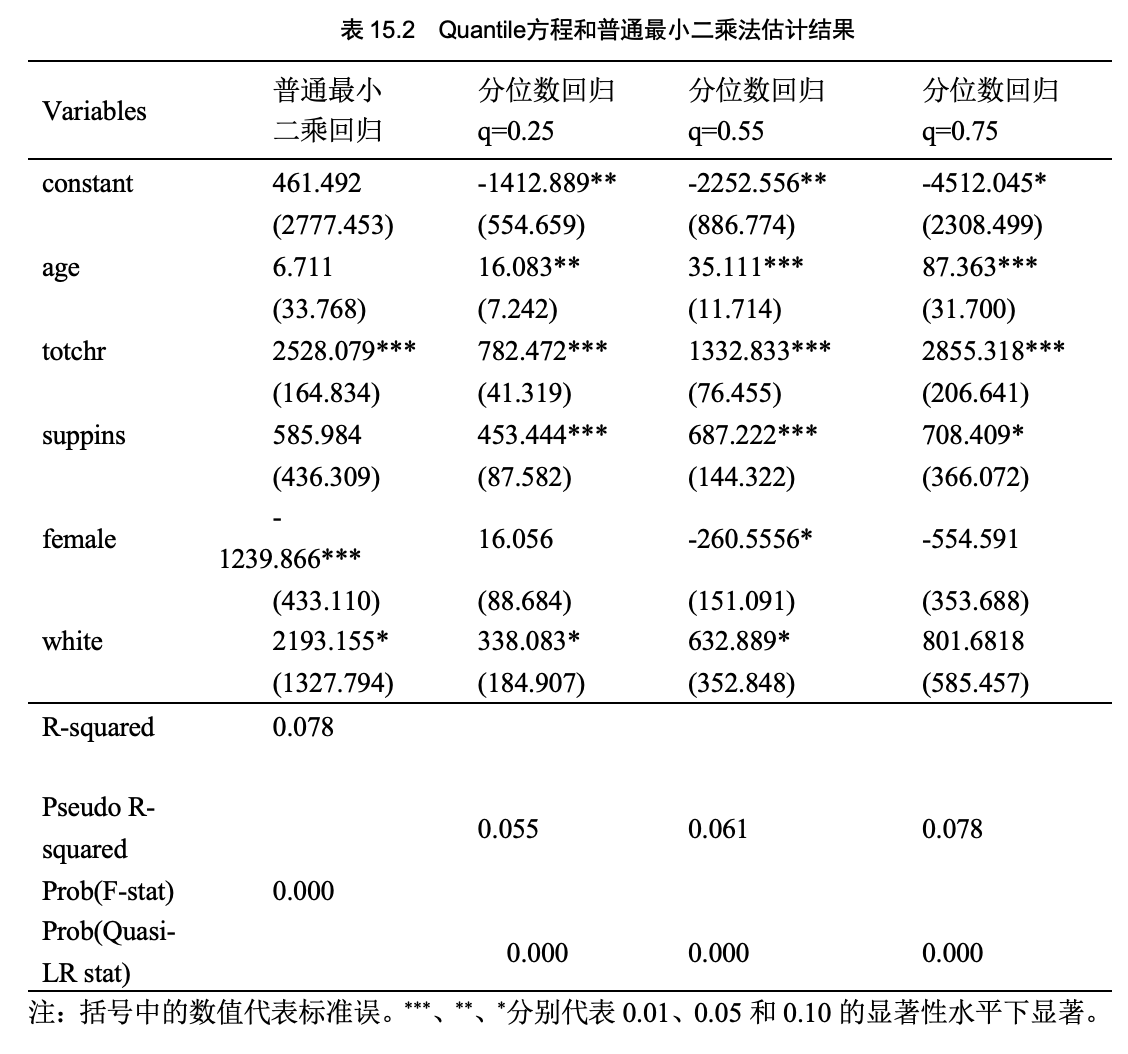
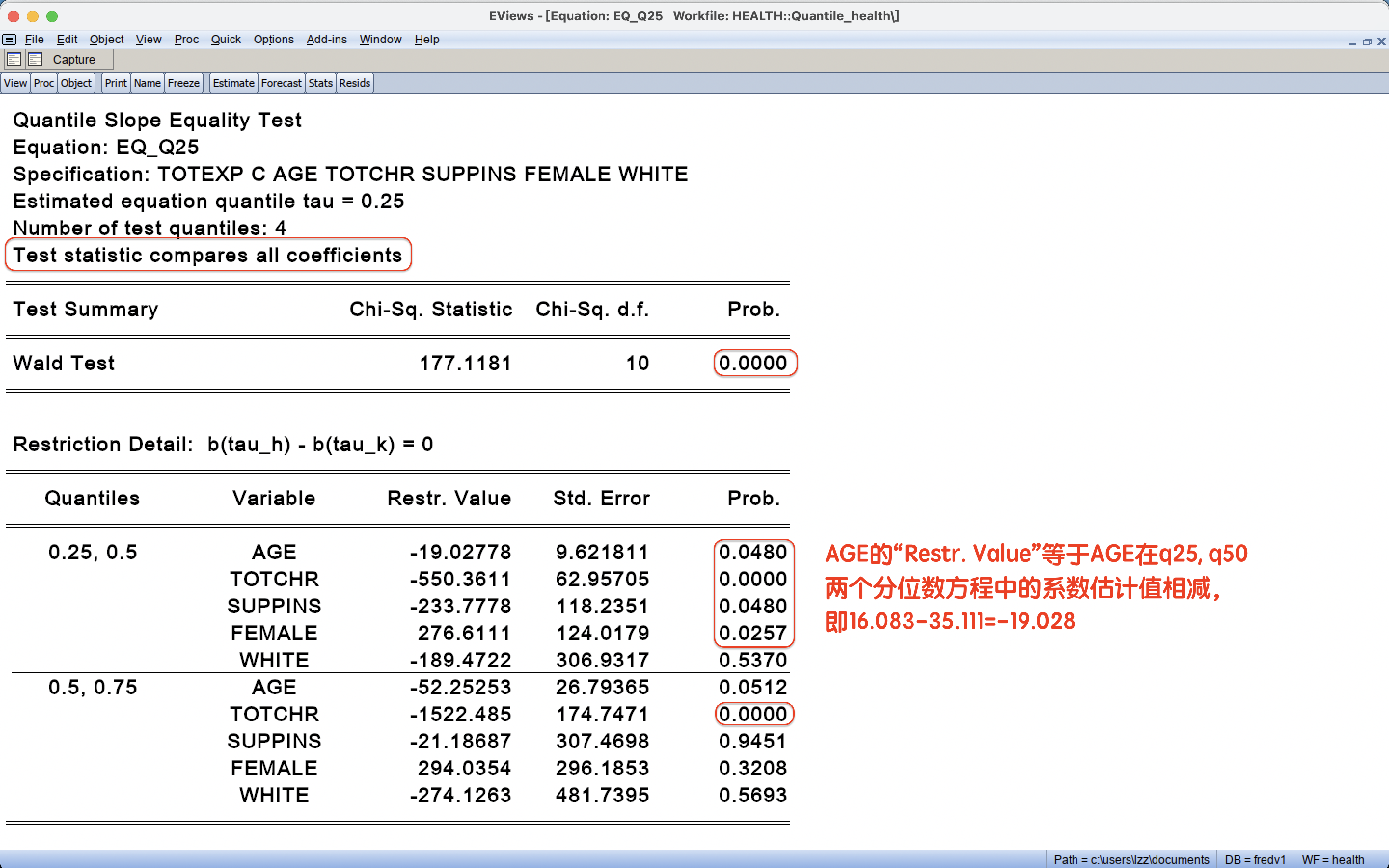
4 分位数回归模型的诊断: 斜率相等检验
检验目的:解释变量对被解释变量的条件分布的影响效应是否存在差异?
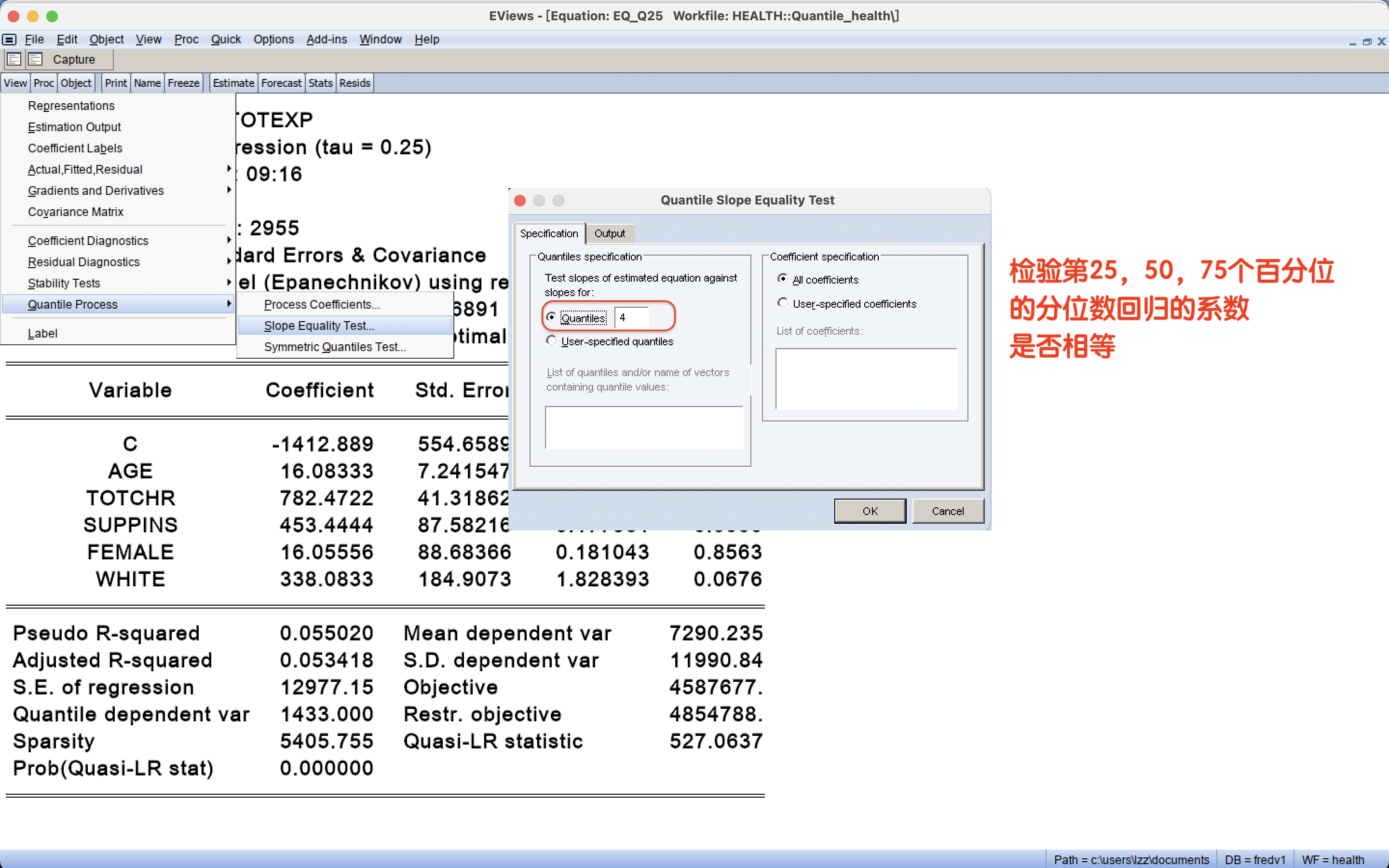
4 分位数回归模型的诊断: 斜率相等检验
4 分位数回归模型的诊断: 对称性检验
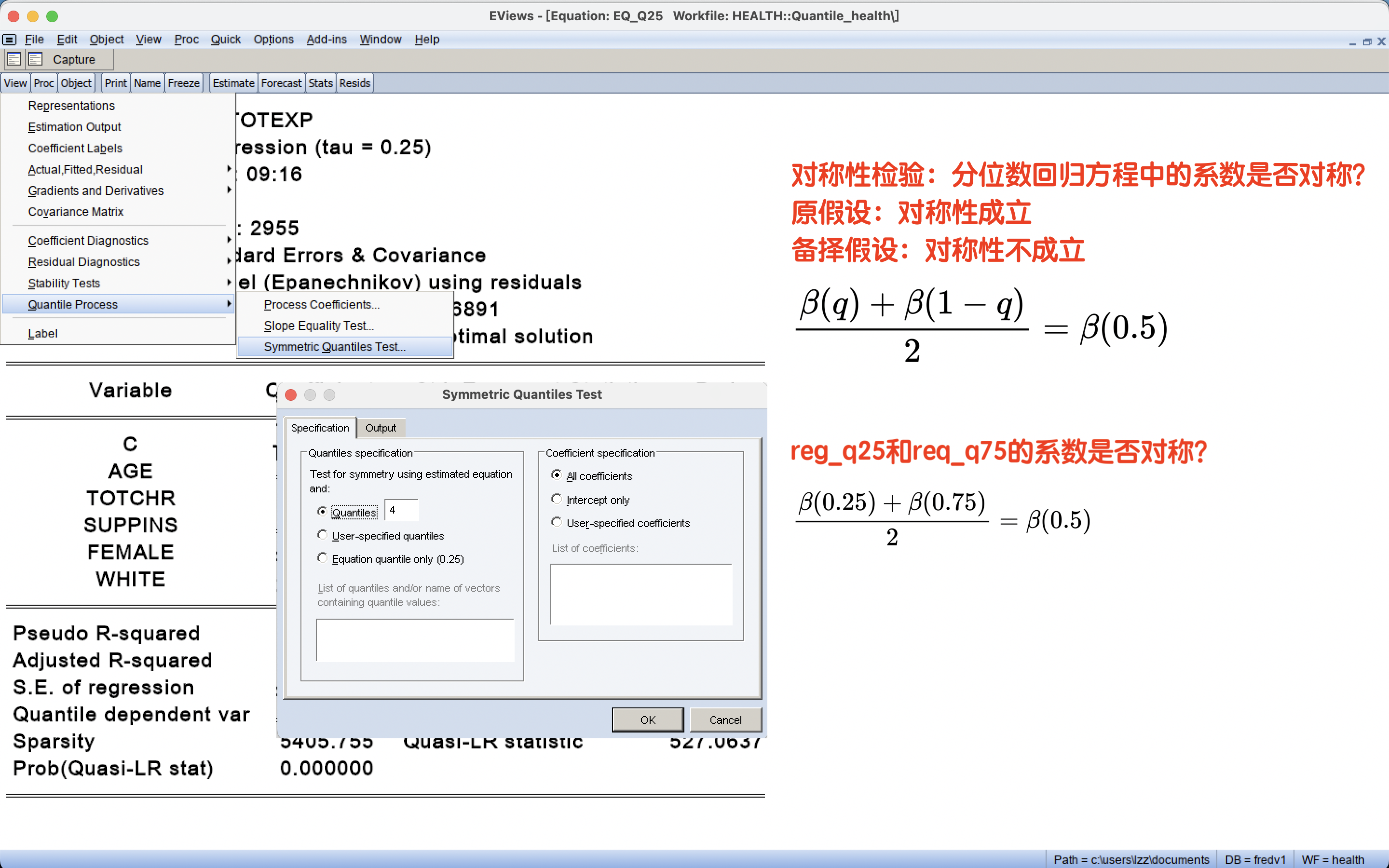
4 分位数回归模型的诊断: 对称性检验
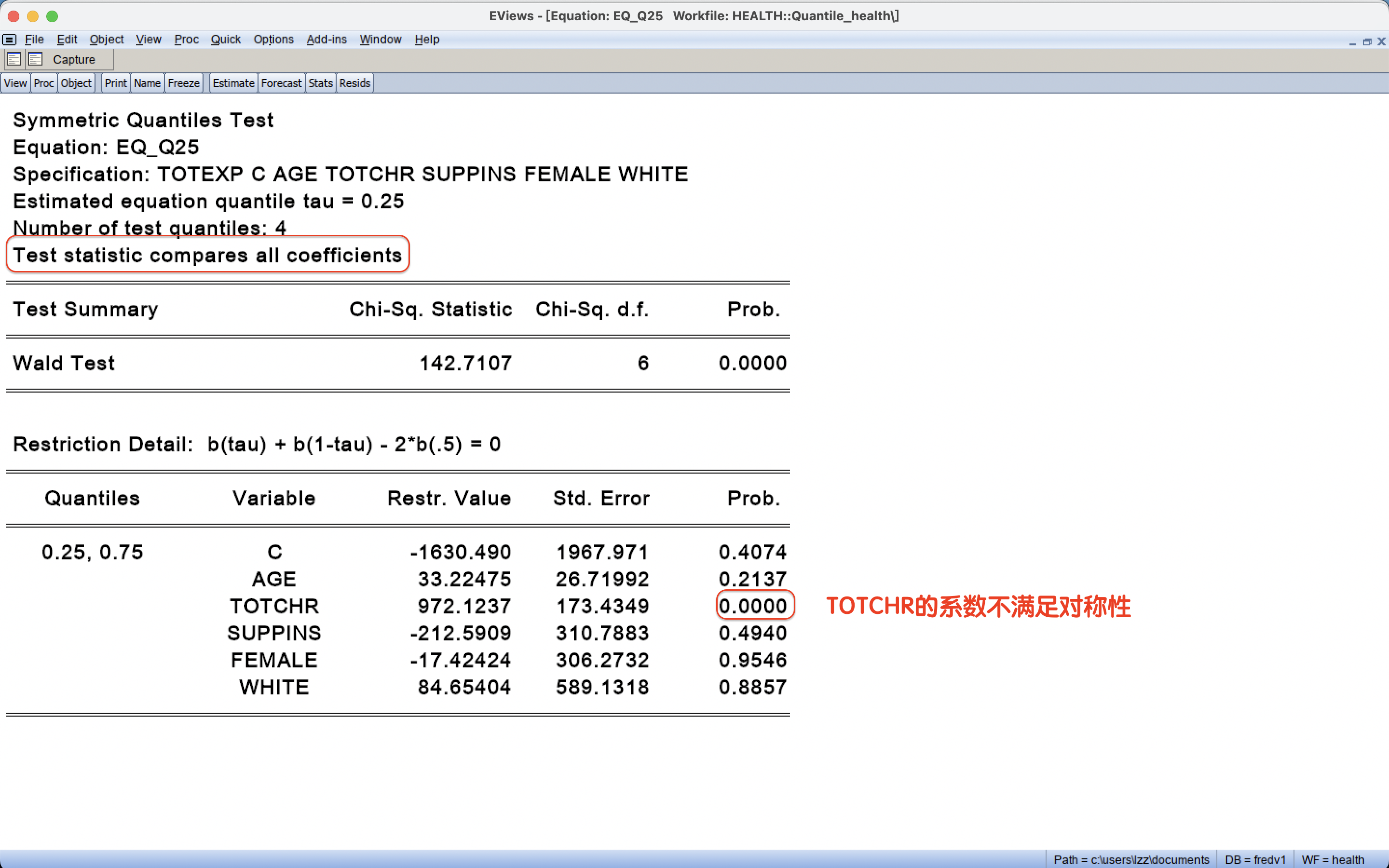
5 分位数回归模型的可视化:过程系数
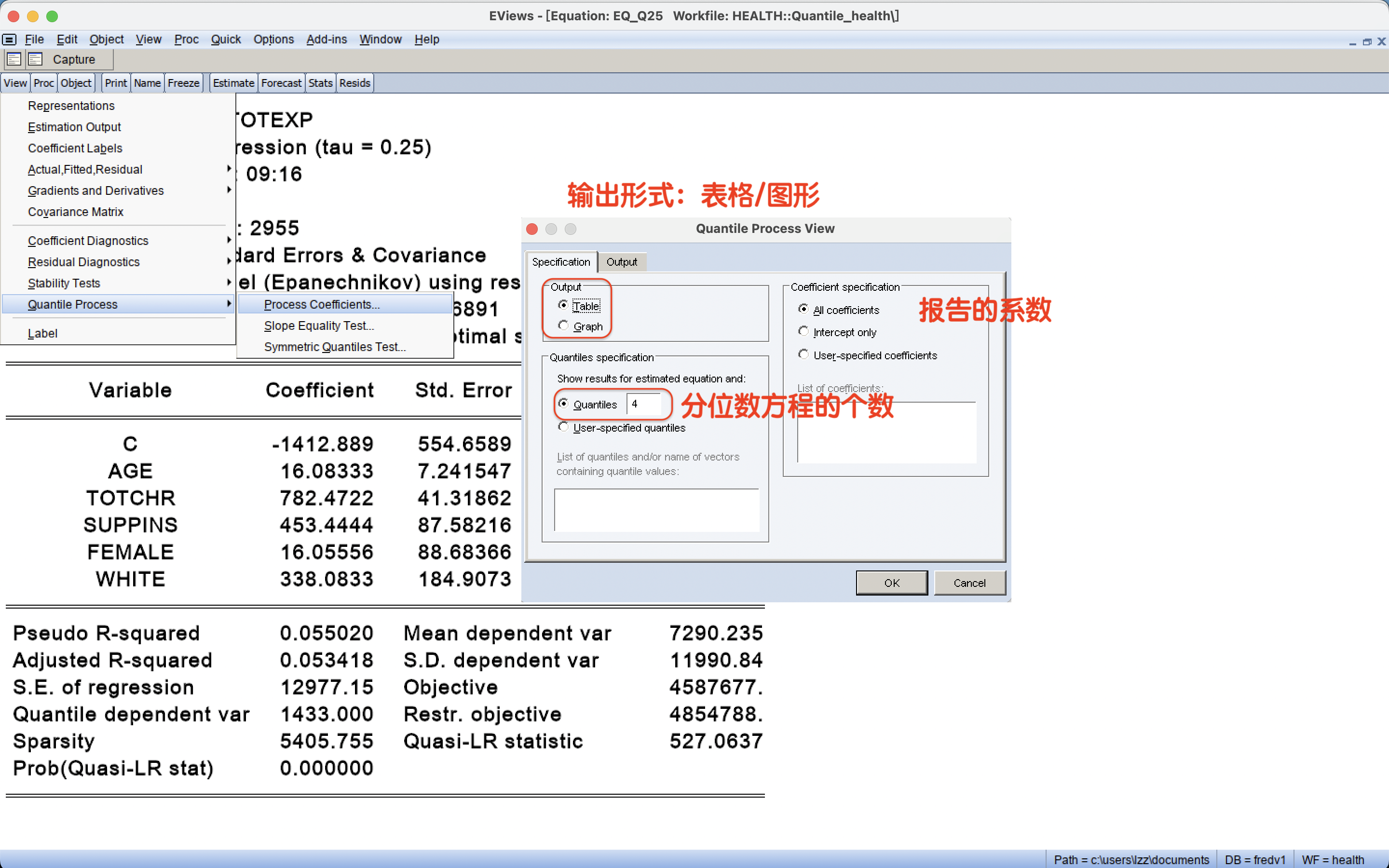
5 分位数回归模型的可视化:系数表格
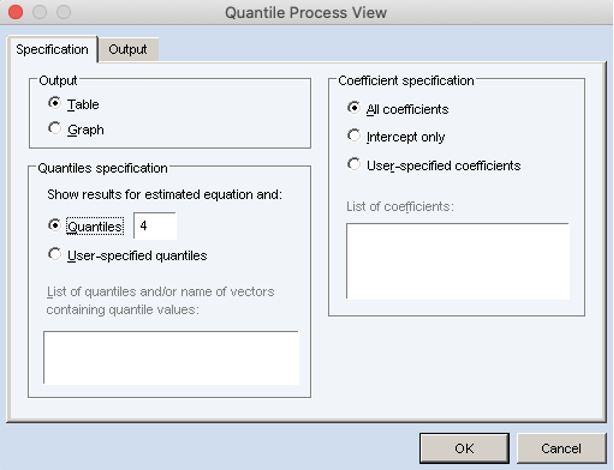
5 分位数回归模型的可视化:系数表格
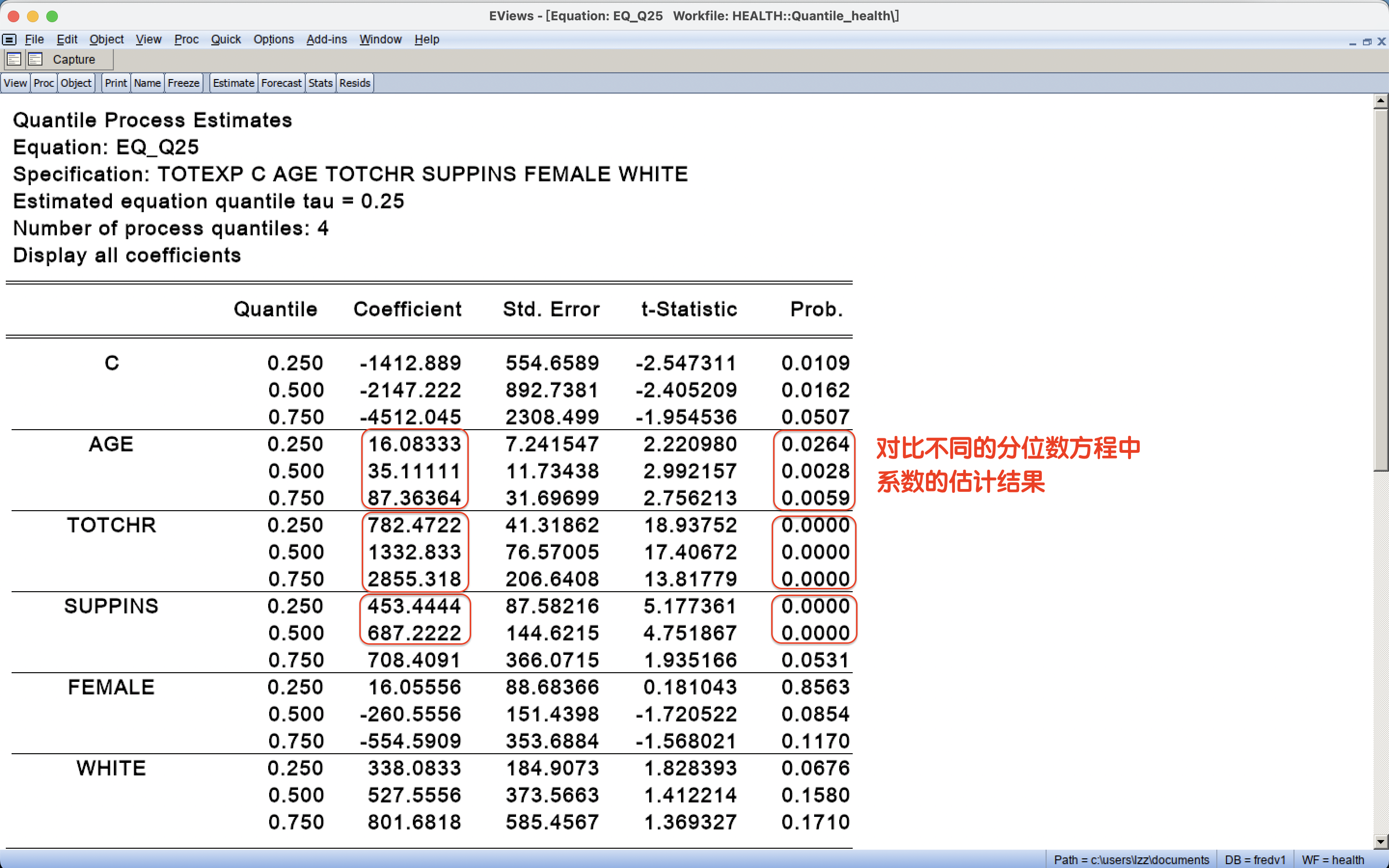
5 分位数回归模型的可视化:系数表格
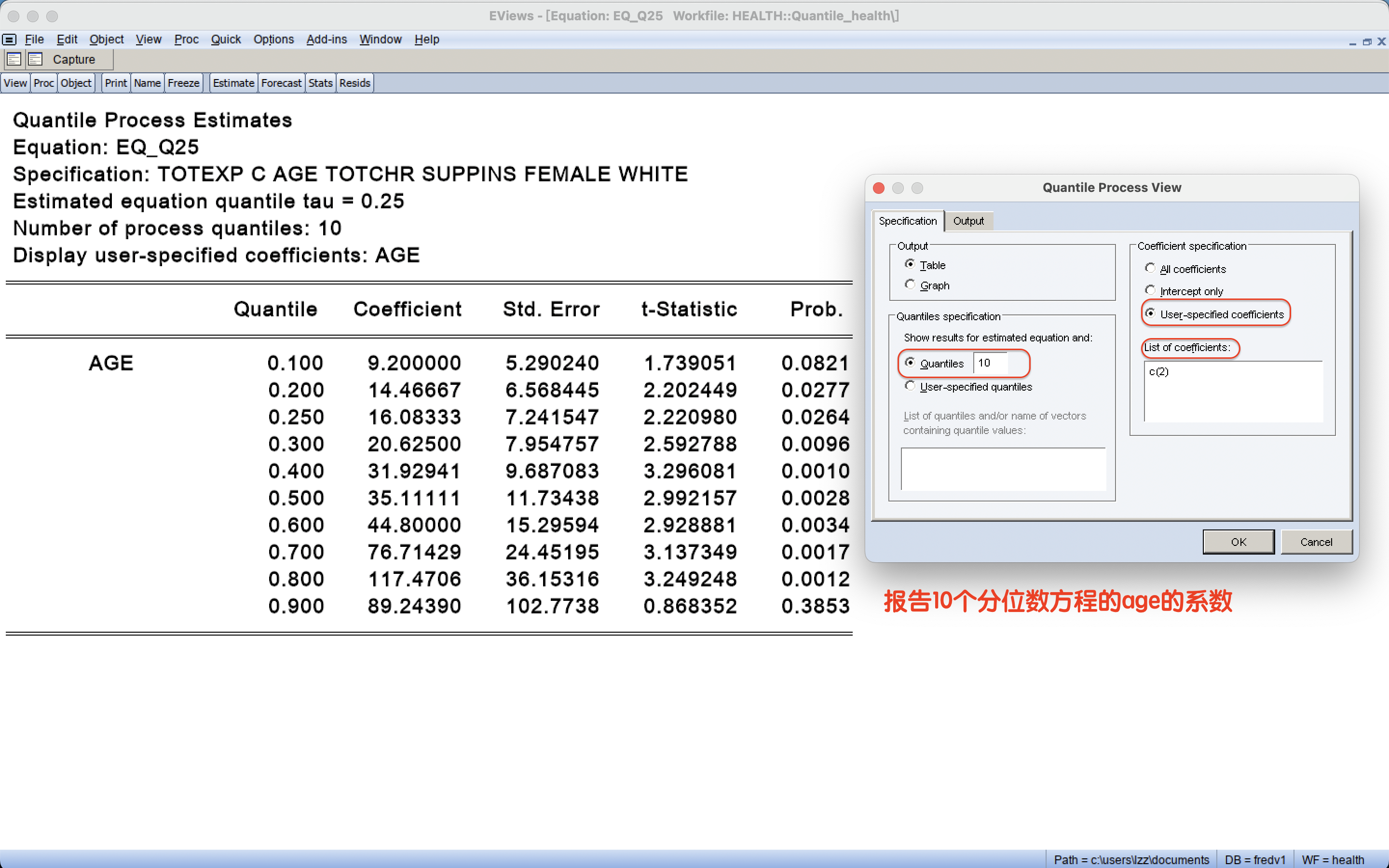
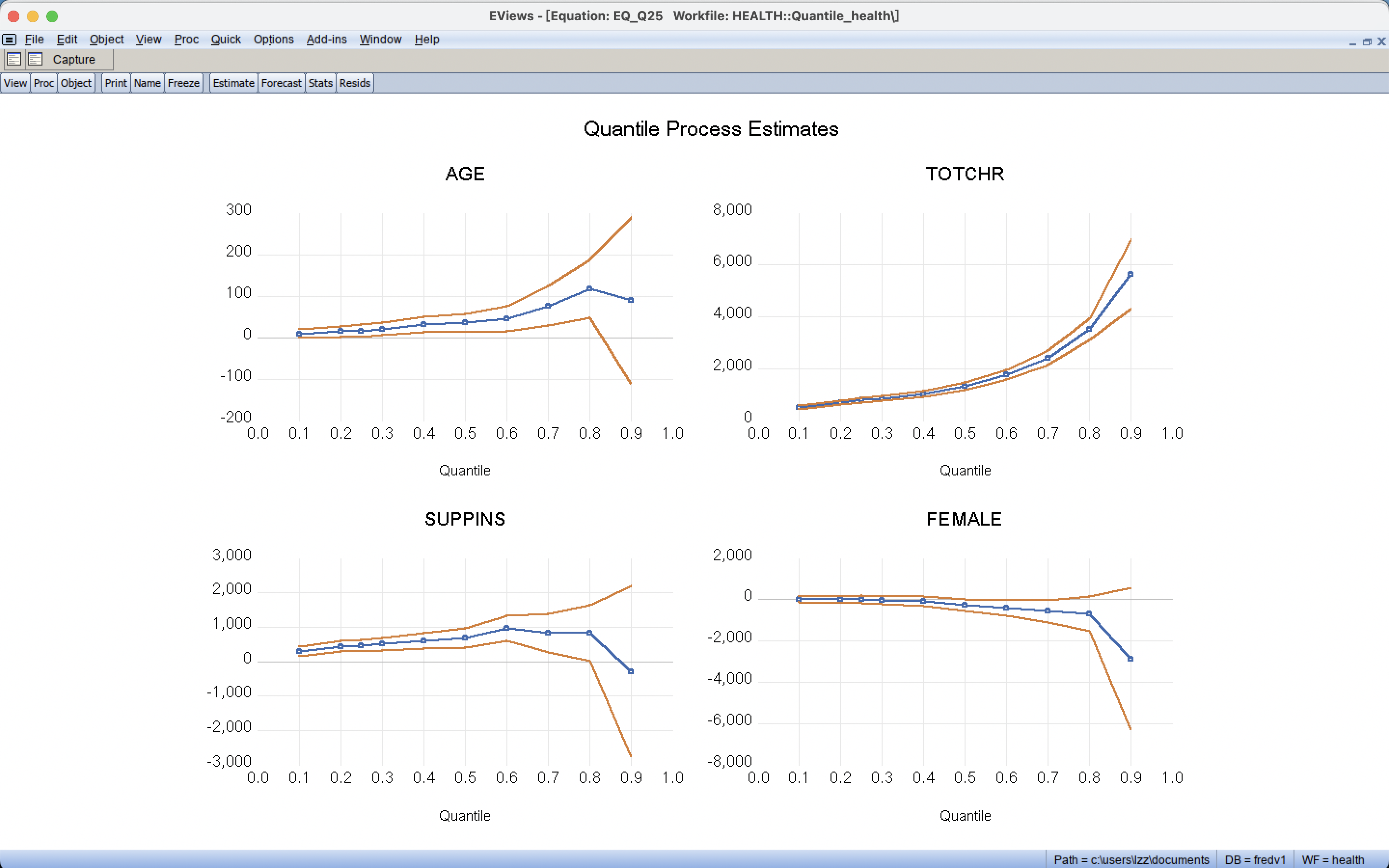
5 分位数回归模型的可视化:系数图像
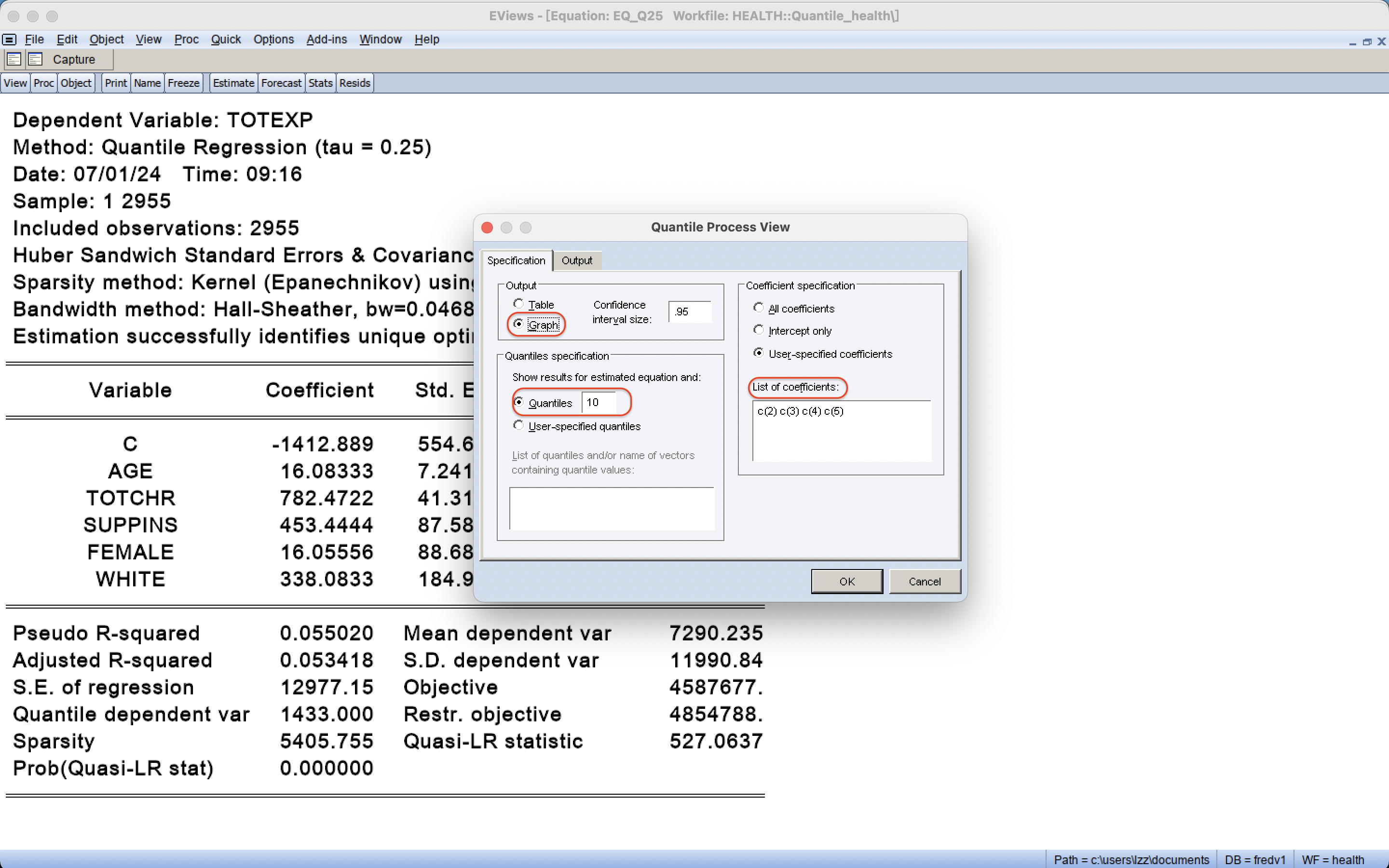
5 分位数回归模型的可视化:系数图像
6 EViews代码:分位数回归方程的估计
估计中位数数方程eq1
equation eq1.qreg totexp c age totchr suppins female white
估计第25个百分位数方程eq1
equation eq1.qreg(quant=0.25) totexp c age totchr suppins female white
6 EViews代码:分位数回归方程的检验
检验eq1方程系数是否相等(检验q25, q50, q75)
eq1.qrslope
eq1方程的系数是否相等检验(检验10个分位数方程)
eq1.qrslope(n=10)
eq1方程的系数的对称性检验(检验q25和q75的对称性)
eq1.qrsymn
eq1方程的系数的对称性检验(检验q10 & q90, q20 & q80, q25& q75, q30 & q70, q40 & q60,的对称性)
eq1.qrsymm(n=10)
6 EViews代码:分位数回归方程可视化
绘制4个分位数方程的所有系数的表格
eq1.qrprocess(n=4)
绘制10个分位数方程的第2个系数的表格
eq1.qrprocess @coefs c(2)
绘制4个分位数方程的所有系数的图像
eq1.qrprocess(n=4, graph)
绘制10个分位数方程的第2个系数、第3个系数的图像
eq1.qrprocess(graph) @coefs c(2) c(3)
7 EViews优势
操作灵活:图形窗口操作/命令行操作
经济计量分析工具的集成
功能丰富的插件
易学易用、不易遗忘
7 EViews使用经验
先窗口操作,再命令行操作
View视图工具的使用
表格的导出