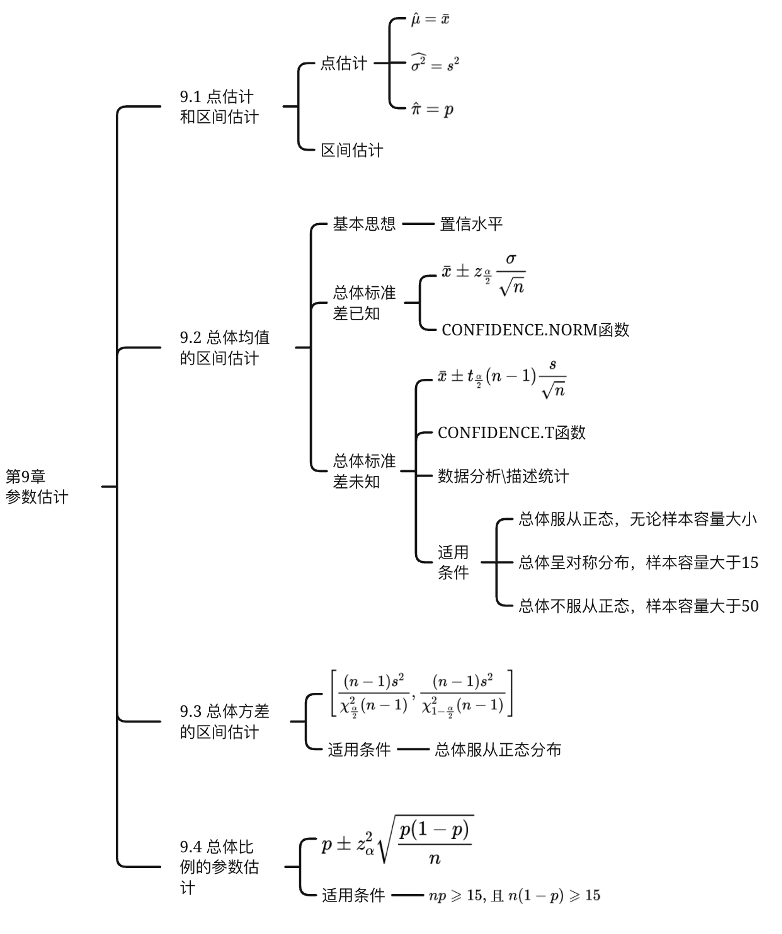
第9章 参数估计

《精通Excel数据统计与分析》

2024-09-27

第9章 参数估计

• 9.1 点估计和区间估计

• 9.2 总体均值的区间估计

• 9.3 总体方差的区间估计

• 9.4 总体比例的区间估计

9.1 点估计和区间估计

• 点估计（Point Estimation）用单个的值来推断总体参数。

• 区间估计（Interval Estimation）为总体参数构造了一个估计区间，不再是用单个的数值来推断总体参数，而是给出一个区间范围，以及还表达了估计的可靠程度。

9.2 总体均值的区间估计

• 9.2.1 基本思想

• 9.2.2 置信水平的理解

• 9.2.3 总体均值的置信区间的计算

9.2.1 基本思想

中心极限定理在样本均值和总体均值之间构建了一座桥梁，样本均值的期望等于总体均值，样本均值是以总体均值为中心而波动的。

9.2.2 置信水平的理解

图9.2 计算100个样本的置信水平为95%的区间估计

9.2.3 总体均值的置信区间的计算

• 总体标准差σ已知

• 总体标准差σ未知

9.2.3 总体均值的置信区间的计算

• 注意

• CONFIDENCE.T函数使用t(n-1)的双侧1-α分位点

• CONFIDENCE.NORM函数使用标准正态分布的1-α分位点。

9.2.3 总体均值的置信区间的计算

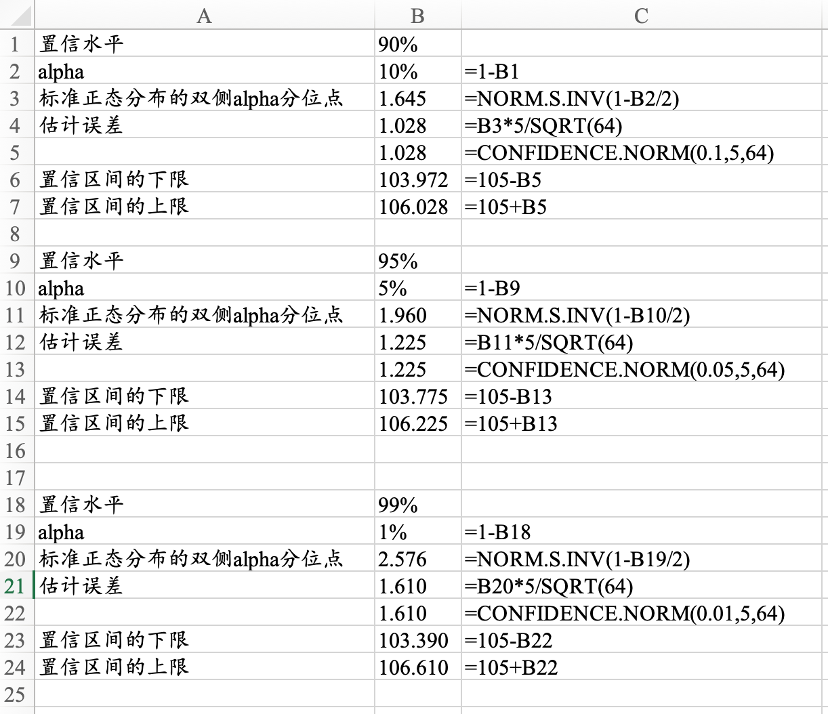
图9.5总体标准差已知，置信水平为90%，95%和99%的总体均值的区间估计

9.2.3 总体均值的置信区间的计算

• 当总体标准差已知时，可利用CONFIDENCE.NORM函数计算估计误差，该函数的第一项参数是1-置信水平，第2项参数是总体标准差，第3项参数是样本容量

• 当总体标准差未知时，可利用CONFIDENCE.T函数计算估计误差，该函数的第一项参数是1-置信水平，第2项参数是样本标准差，第3项参数是样本容量。

• 当总体标准差未知时，单击“数据” →“数据分析” →“描述统计”， 在“平均数置信度”中填入置信水平，可以计算估计误差。

9.3 总体方差的区间估计

• 9.3.1 总体方差的置信区间的构造

• 9.3.2 实践应用

9.3.1 总体方差的置信区间的构造

9.3.2 实践应用

• 在实践中，研究者不仅关心数据分布的中心，也关注数据分布的波动程度。

• 在质量控制领域，会对元件的规格、耐用寿命的均值、方差有严格的标准。

9.4 总体比例的区间估计

• 9.4.1 总体比例的置信区间的构造

• 9.4.2 实践应用

9.4.1 总体比例的置信区间的构造

9.5 本章总结

本章总结