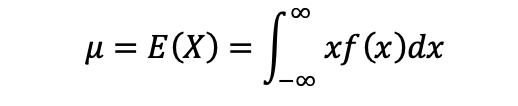第7章 连续型随机变量的分布

《精通Excel数据统计与分析》

2024-09-27

第7章 连续型随机变量的分布

  • 7.1 关键概念

  • 7.2 均匀分布

  • 7.3 正态分布

  • 7.4 卡方分布

  • 7.5 t分布

  • 7.6 F分布

  • 7.7 指数分布

7.1 关键概念

  • 7.1.1 连续型随机变量

  • 7.1.2 概率密度函数

  • 7.1.3 累积分布函数

  • 7.1.4 连续型随机变量的期望和方差

7.1.1 连续型随机变量

连续型随机变量是指随机变量在一定范围内可以取无限多个值，无法一一列举其取值。

7.1.2 概率密度函数

  • 概率密度函数（Probability Density Function，简称PDF），描述了连续型随机变量X的分布

7.1.2 概率密度函数的性质

7.1.3 累积分布函数

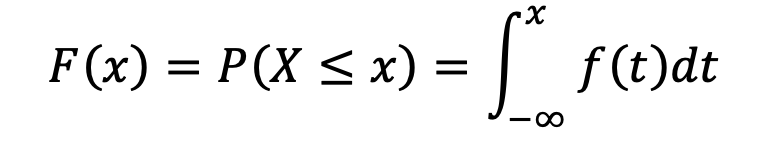
7.1.4 连续型随机变量的期望和方差

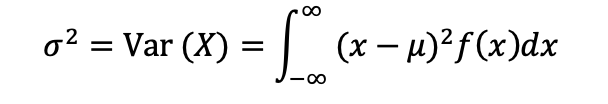
7.2 均匀分布

  • 均匀分布的概率密度函数

  • 均匀分布的累积分布函数

  • 均匀分布的期望和方差

7.2 均匀分布的概率密度函数

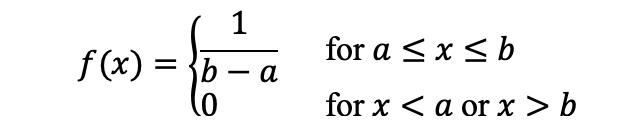
7.2 均匀分布的累积分布函数

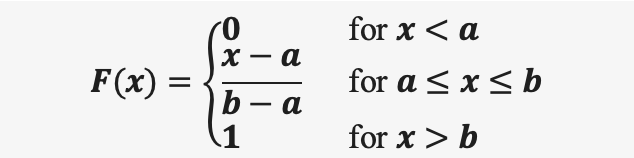
7.2 均匀分布的期望和方差

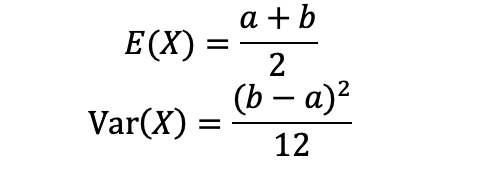
7.3 正态分布

正态分布的概率密度函数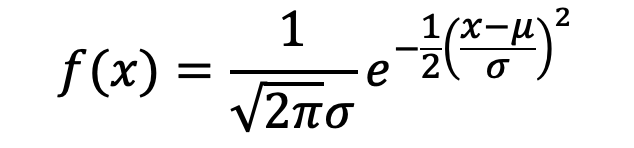

7.3.3 正态分布的应用

  • 7.3.1 正态分布的性质

  • 7.3.2 Excel绘制正态分布的PDF和CDF

  • 7.3.3 正态分布的应用

7.3.1 正态分布的性质

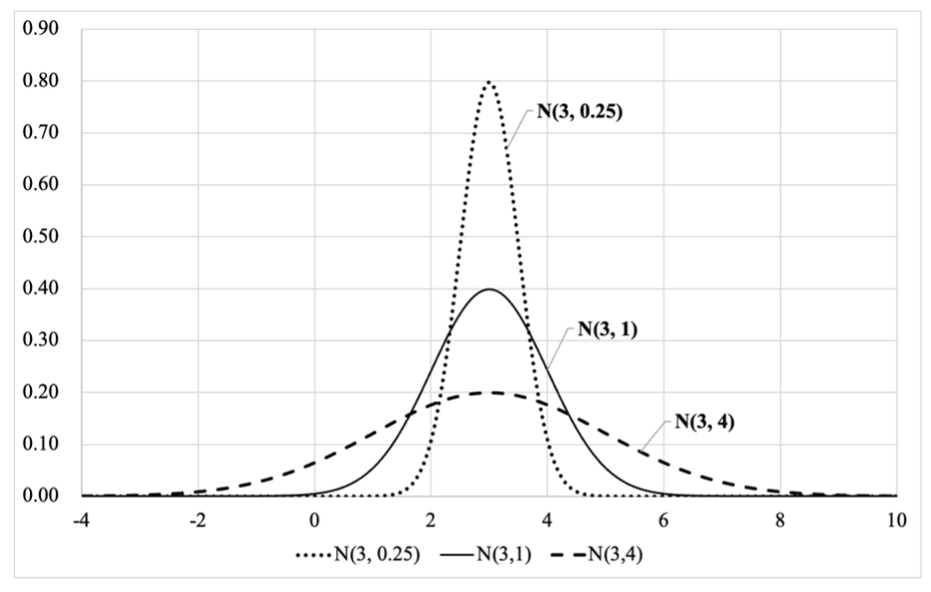
图7.3 均值相同，标准差不同的正态分布概率密度曲线

7.3.1 Excel实操技巧

  • 在NORM.DIST函数中，将最后一项参数设置为“FALSE”，计算正态分布的概率密度函数的值；最后一项参数设置为“TRUE”，计算正态分布的累积分布函数的值，即服从正态分布的随机变量小于等于指定值的概率。

  • 在NORM.S.DIST函数中，将最后一项参数设置为“FALSE”，计算标准正态分布概率密度函数的值；最后一项参数设置为“TRUE”，计算标准正态分布的累积分布函数的值，即服从标准正态分布的随机变量小于等于指定值的概率。

7.3.2 Excel绘制正态分布的PDF和CDF

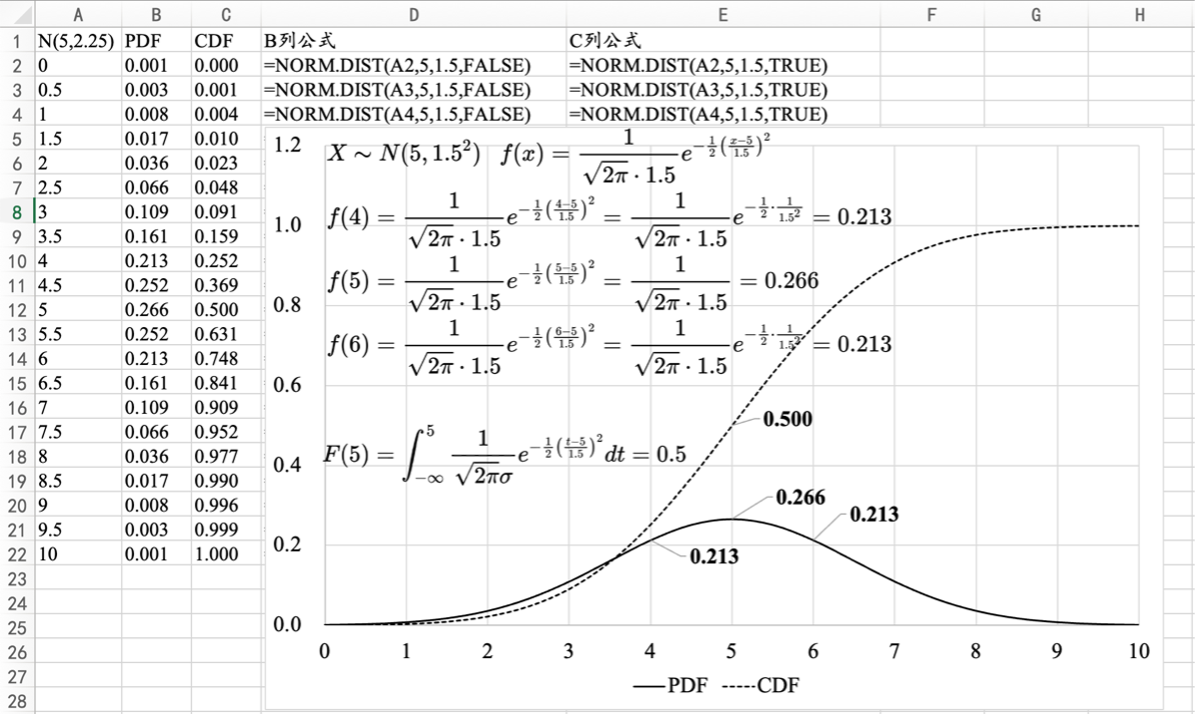
图7. 9 正态分布的PDF和CDF曲线

7.3.3 正态分布的应用

  • 诊断数据中是否存在异常值

  • 计算服从正态分布的随机变量落在特定区间的概率

  • 给定服从正态分布的随机变量落在某个区间的概率，求该区间。

  • 诊断数据是否服从正态分布

正态分布Excel实操技巧

  • NORM.INV函数适用于普通的正态分布，有三项参数，依次是左尾概率1-α、均值μ和标准差σ，可以求出正态分布N(μ,σ^2 )的上α分位点。

  • NORM.S.INV函数只适用于标准正态分布，给定左尾概率1-α，可以求出标准正态分布的上α分位点。

7.4 卡方分布

  • 7.4.1 卡方分布的性质

  • 7.4.2 EXCEL绘制卡方分布的PDF和CDF

  • 7.4.3 卡方分布的应用

7.4.1 卡方分布的性质

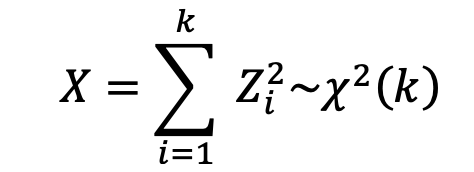
7.4.1 卡方分布的性质

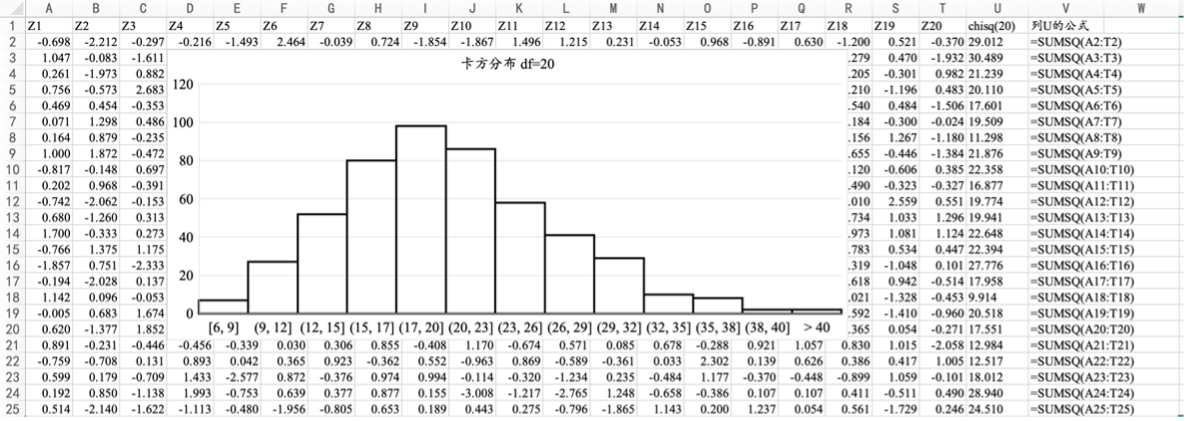
7.4.2 EXCEL绘制卡方分布的PDF和CDF

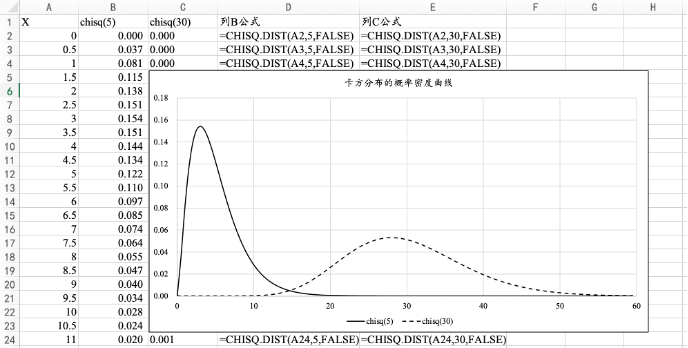
图7.17 服从χ^2 (20)的500个随机数的直方图

7.4.3 卡方分布的应用

  • 总体方差的置信区间的构造

  • 总体方差的参数检验

  • 独立性检验

7.5 t分布

  • 7.5.1 t分布的性质

  • 7.5.2 EXCEL绘制t分布的PDF和CDF

  • 7.5.3 t分布的应用

7.5.1 t分布的性质

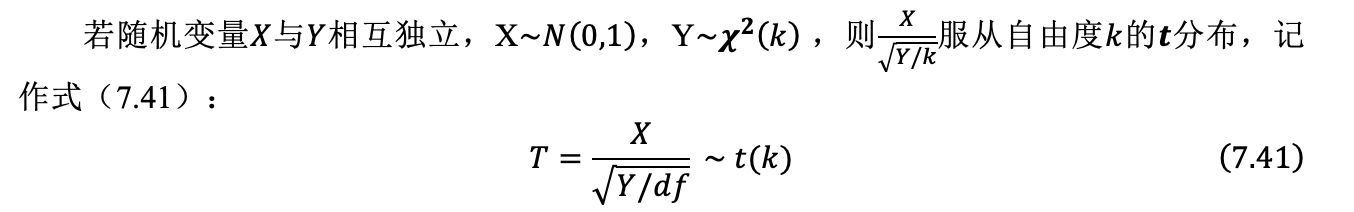
7.5.2 EXCEL绘制t分布的PDF和CDF

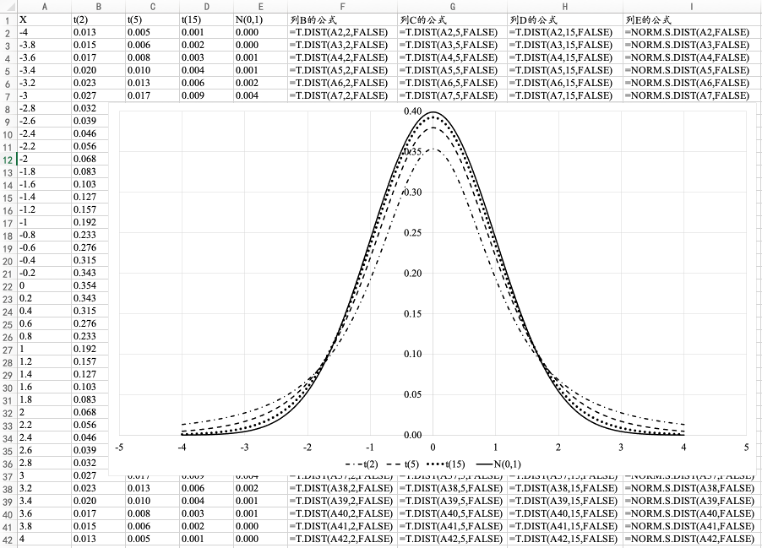
图7.23 t(2)、t(5)、t(15)和N(0,1)的概率密度曲线

7.5.3 t分布的应用

  • 总体均值的置信区间的构造

  • 总体均值的参数检验

  • 两个总体均值的参数检验

7.6 F分布

  • 7.6.1 F分布的性质

  • 7.6.2 EXCEL绘制F分布的PDF和CDF

  • 7.6.3 F分布的应用

7.6.1 F分布的性质

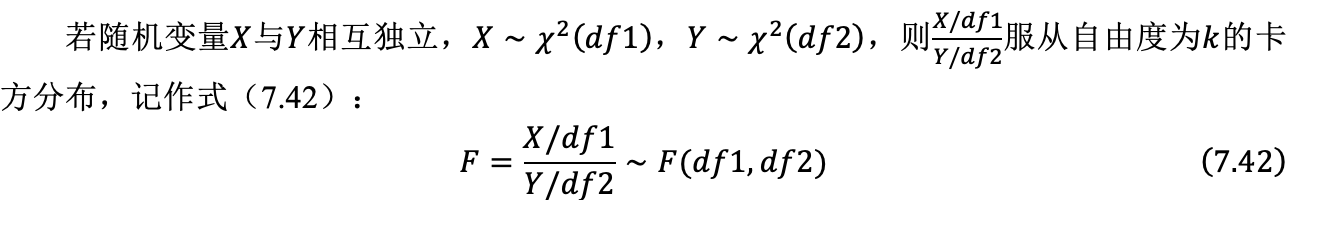
7.6.2 EXCEL绘制F分布的PDF和CDF

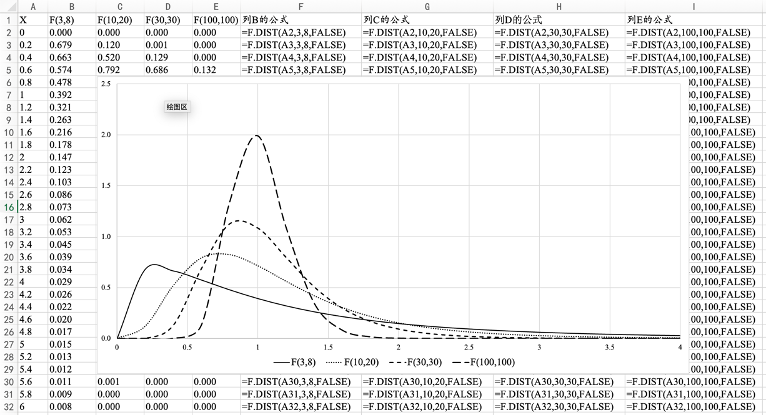
图7.27 F(3,8)、F(10,20)、F(30,30)、F(100,1000)的概率密度曲线

7.6.3 F分布的应用

  • 两个总体的方差比的检验

  • 方差分析

7.7 指数分布

  • 7.7.1 指数分布的性质

  • 7.7.2 EXCEL绘制指数分布的PDF和CDF

  • 7.7.3 指数分布的应用

7.7.1 指数分布的性质

7.7.2 EXCEL绘制指数分布的PDF和CDF

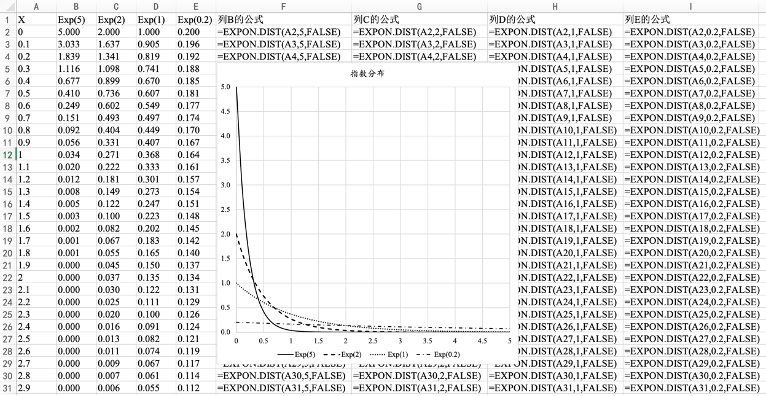
图7.29 “Exp”(5)、“Exp”(2)、“Exp”(1)、“Exp”(0.2)的概率密度曲线

7.7.3 指数分布的应用

  • 排队问题

  • 到银行柜台办理业务的顾客到达的时间间隔的分布

  • 急救中心收到的呼救电话的时间间隔的分布

本章总结

https://lizongzhang.github.io/excelstat