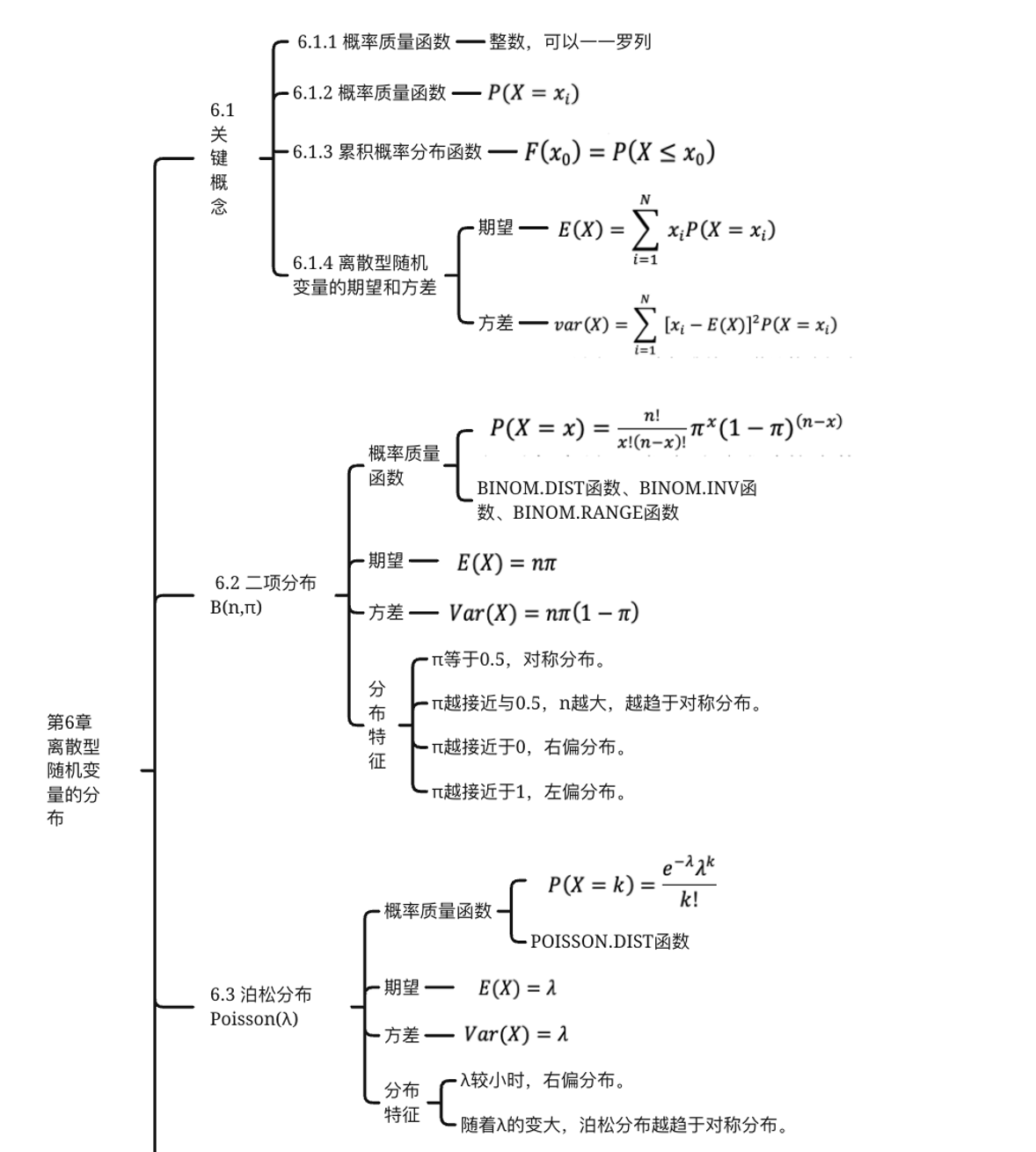
第6章 离散型随机变量的分布

《精通Excel数据统计与分析》

2024-09-27

第6章 离散型随机变量的分布

  • 6.1 关键概念

  • 6.2 二项分布

  • 6.3 泊松分布

6.1 关键概念

  • 6.1.1 离散型随机变量

  • 6.1.2 概率质量函数

  • 6.1.3 累积概率分布函数

  • 6.1.4 离散型随机变量的期望和方差

6.1.1 离散型随机变量

  • 离散型随机变量的取值通常表现为整数。

  • 随机变量的取值并不直接表现为数值，例如餐厅顾客的性别，其结果为男性或女性，但可将男性赋值为1，女性赋值为0，将文本类型的取值转换为一个数值代码，此类随机变量也是离散型随机变量。

6.1.2 概率质量函数

概率质量函数（Probability Mass Function，简称PMF），描述了离散型随机变量取特定数值的概率。

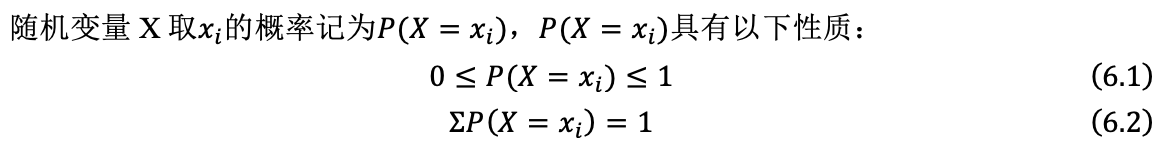
6.1.3 累积概率分布函数

累积概率分布函数（Cumulative Probability Distribution Functiaon, 简称CDF。

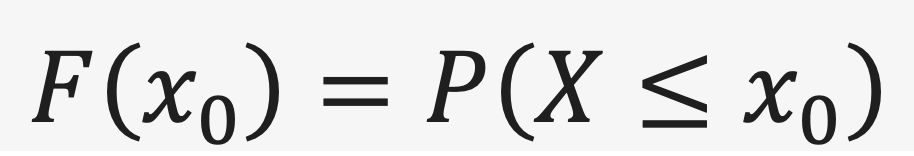
累积概率分布函数

6.1.4 离散型随机变量的期望和方差

  • 离散型随机变量变量的期望（Expected Value，或者Expectance）代表了随机变量分布的中心，将随机变量的某个取值乘以取该值的概率，这些乘积项的和等于期望。

6.1.4 离散型随机变量的期望和方差

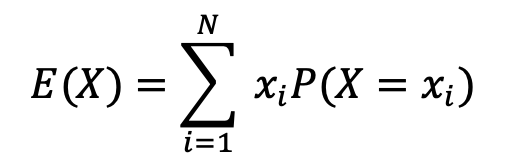
期望的计算式

6.1.4 离散型随机变量的期望和方差

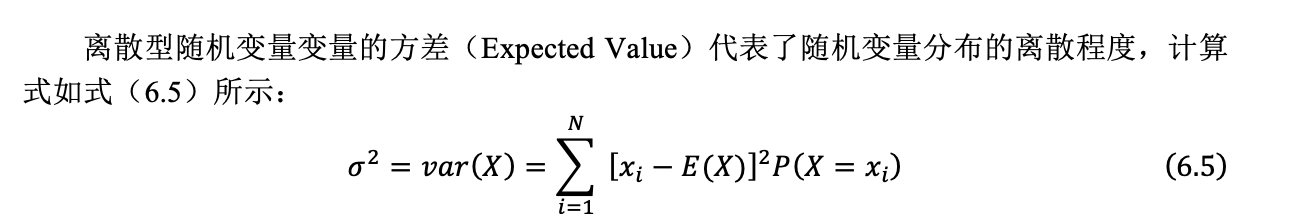
方差的计算式

6.2 二项分布

  • 6.2.1 二项分布的性质

  • 6.2.2 Excel计算二项分布的取值概率

  • 6.2.3 Excel绘制二项分布的图像

6.2.1 二项分布的性质

  • 二项分布的假定

  • 二项分布的概率质量函数

  • 二项分布的期望和方差

6.2.1 二项分布的概率质量函数

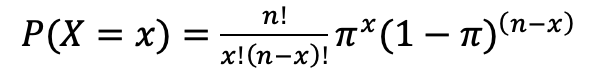
6.2.1 二项分布的期望和方差

6.2.2 Excel计算二项分布的取值概率

  • BINOM.DIST函数

6.2.3 Excel绘制二项分布的图像

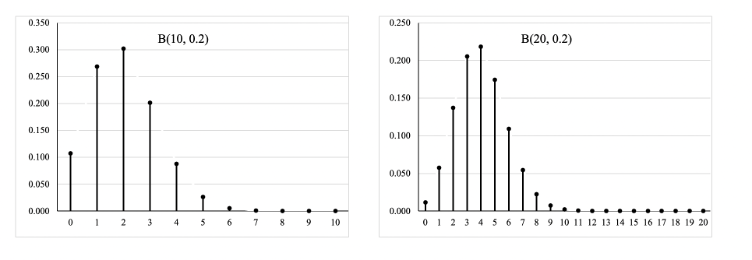
6.3 泊松分布

  • 6.3.1 泊松分布的性质

  • 6.3.2 泊松分布与二项分布的关系

  • 6.3.3 Excel计算泊松分布的取值概率

  • 6.3.4 Excel绘制泊松分布的图像

6.3.1 泊松分布的性质

  • 泊松分布的假定

  • 泊松分布的概率质量函数

  • 泊松分布的期望和方差

  • 泊松分布的应用场景

6.3.1 泊松分布的概率质量函数

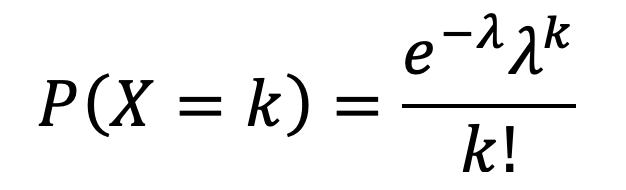
6.3.1 泊松分布的期望和方差

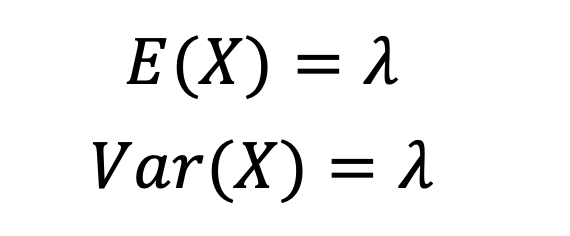
6.3.2 泊松分布与二项分布的关系

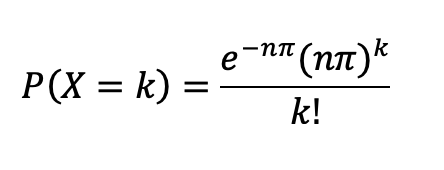
6.3.3 Excel计算泊松分布的取值概率

  • POISSON.DIST函数

6.3.4 Excel绘制泊松分布的图像

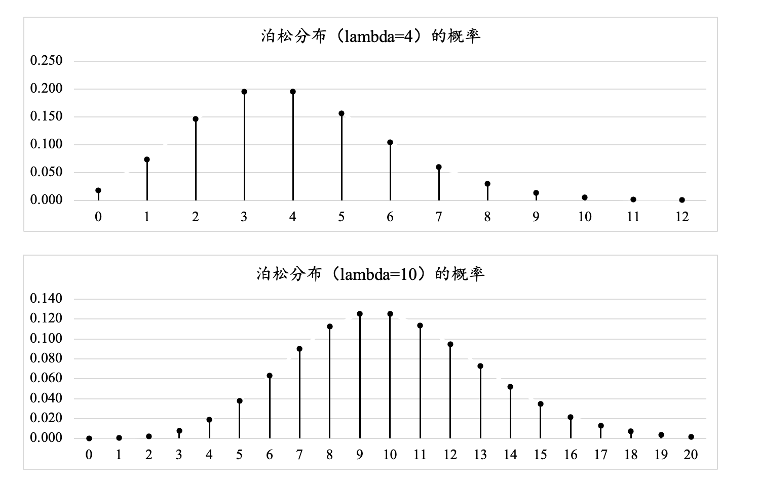
图6.9 Poisson(4)和Poisson(10)的概率质量函数图像

本章总结

https://lizongzhang.github.io/excelstat