第16章 时间序列

《精通Excel数据统计与分析》

2024-09-27

第16章 时间序列

  • 16.1 描述性分析

  • 16.2 平稳序列

  • 16.3 非平稳序列

  • 16.4 复合型时间序列

  • 16.5 三段式指数平滑法

16.1 描述性分析

  • 16.1.1 长期趋势

  • 16.1.2 季节变动

  • 16.1.3 循环变动

  • 16.1.4 不规则变动

16.1.1 长期趋势

  • 长期趋势（Long-term Trend）是时间序列中呈现出来的持续性的变动趋势。

16.1.2 季节变动

  • 季节变动（Seasonal Variation）是指由于自然气候、风俗习惯等造成的时间序列的周期性波动。

  • 季节变动的周期长度通常小于1年，具有较强的规律性，从时序图中可以发现季节变动成分。

16.1.3 循环变动

  • 循环变动（Cyclical Variation）是指时间序列围绕长期趋势的有规律的起伏波动。

  • 循环波动的成因比较复杂，周期的长度不固定。

16.1.4 不规则变动

  • 不规则变动（Irregualr Variation）是指时间序列中剥离了长期趋势、季节变动、循环变动三种成分后剩下的部分。

  • 不规则变动是由于各种各样的随机因素共同作用的，其变化特征不可预见。

16.2 平稳序列

  • 16.2.1 平稳序列的识别

  • 16.2.2 移动平均法

  • 16.2.3 指数平滑法

16.2.1 平稳序列的识别

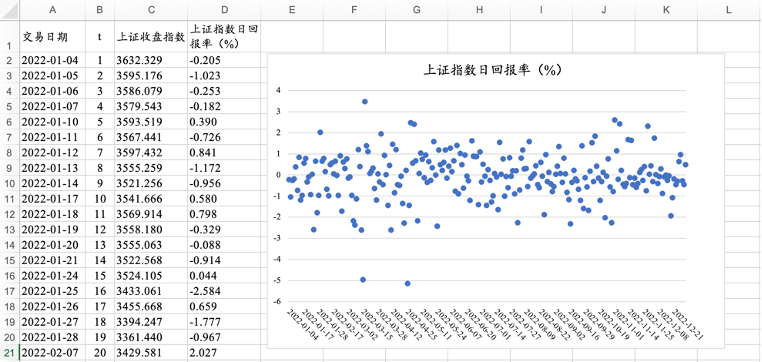
图16.5 2022年242个交易日的上证指数日回报率的时序图

16.2.2 移动平均法

  • 将最近几期观测值的平均值作为下一期的预测值。

  • 若使用最近3期观测值的平均值，作为下一期的预测，就称作3期移动平均，记作MA(3)。

16.2.2 移动平均法

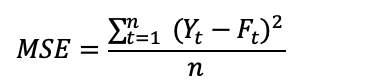
16.2.2 移动平均法

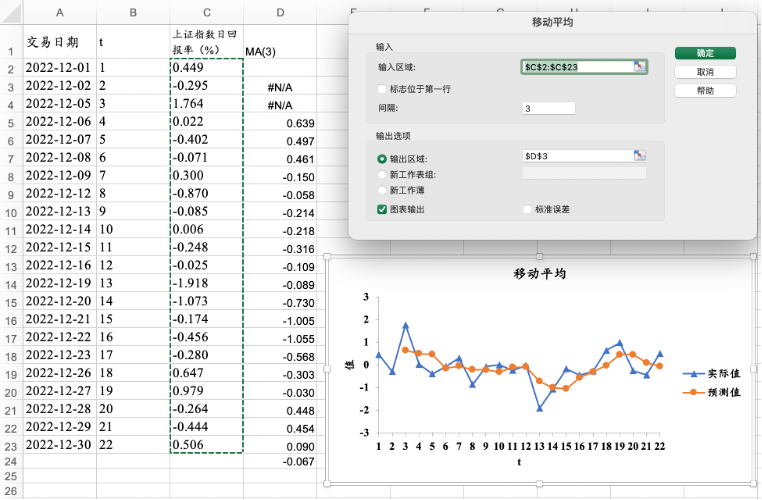
图16.9 数据分析工具中的“移动平均”

16.2.3 指数平滑法

  • 指数平滑法（Smoothing Exponential）和移动平均法其核心思想都是采用修匀技术消除序列的不规则变动。

  • 移动平均采用的是逐期求平均的修匀技术，指数平滑则采用对历史数据进行加权平均的修匀技术。

16.2.3 指数平滑法

16.2.3 指数平滑法

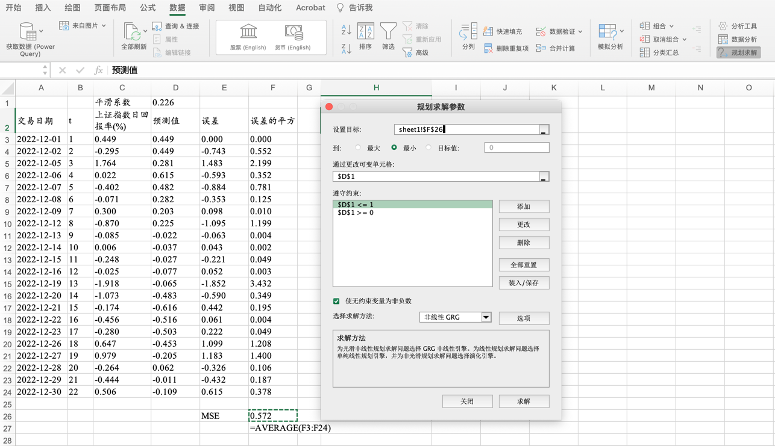
图16.11 “规划求解参数”对话框的设置

16.3 非平稳序列

  • 16.3.1 线性趋势分析

  • 16.3.2 非线性趋势分析

  • 16.3.3 阶段性分析

16.3.1 线性趋势分析

16.3.1 线性趋势分析

  • 实操技巧

  • 绘制时间序列的时间编号和观测值的散点图，在散点图中单击散点，单击右键，在弹出的列表中选择“添加趋势线…”，选择“线性”，勾选“显示公式”和“显示R平方值”，报告线性趋势方程。

  • FORECAST.LINEAR函数可以利用估计的回归方程对时间序列进行预测。

16.3.2 非线性趋势分析

  • 对数线性回归方程

  • 二次项回归方程

16.3.2 非线性趋势分析

  • 实操技巧

  • 在对数线性模型中，可以先将时间序列的观测值取自然对数，然后绘制时间编号与对数序列的散点图，再添加线性趋势线。

  • 若时间序列的时序图呈现U型或者倒U型变化趋势，可以在时序图中添加多项式趋势线，将阶数设定为2。

16.3.3 阶段性分析

  • 时间序列的变化趋势可能呈现阶段性变换，在不同阶段其变化趋势有着显著差异，可以在回归模型中引入反映不同阶段的虚拟变量。

16.3.3 阶段性分析

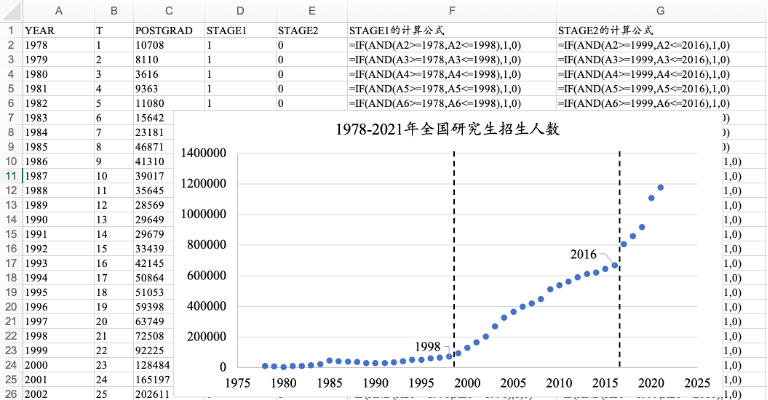
图16. 19 创建虚拟变量STAGE1和STAGE2

16.4 复合型时间序列

  • 16.4.1 因素分解法

  • 16.4.2 乘法模型

16.4.1 因素分解法

  • 因素分解法的核心思想

  • 将时间序列中的长期趋势、季节变动、循环变动和不规则变动四种成分分离出来，通过研究每种成分的特征，进而发现时间序列的变动规律。

16.4.1 因素分解法

16.4.2 乘法模型

图16.23 2016年第1季度至2019年第4季度全国工业企业手机季度销售量的时序图

16.4.2 乘法模型

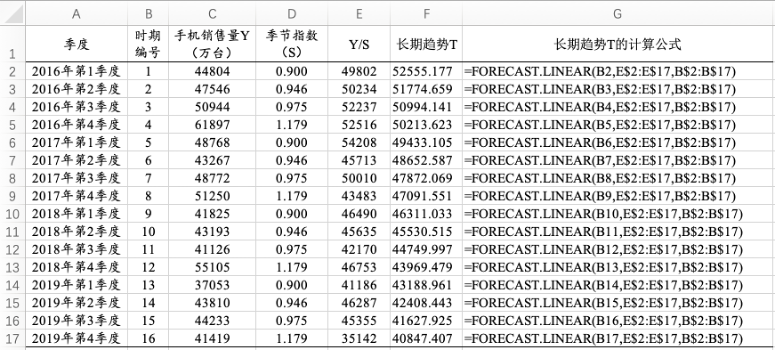
图16.29 FORECAST.LINEAR函数计算长期趋势的预测值

16.5 三段式指数平滑法

  • 16.5.1 模型设定

  • 16.5.2 FORECAST.ETS函数

  • 16.5.3 “预测工作表”工具

16.5.1 模型设定

  • 美国学者Holt在1957年开创性地提出了指数平滑法。

  • 1960年Holt的学生Winters从信号理论中得到启发，提出了三段式指数平滑（Triple Exponential Smoothing）法，因此该方法也被称Holt-Winters方法。

16.5.2 FORECAST.ETS函数

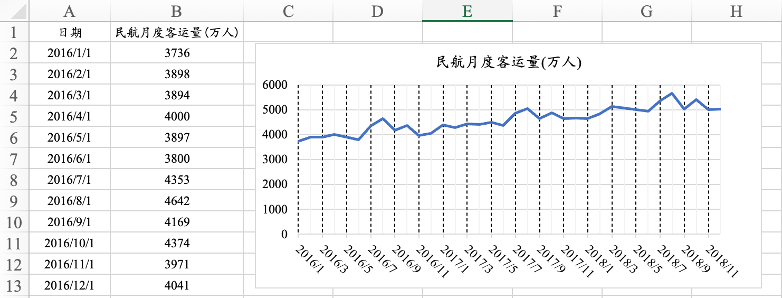
图16. 33 2016年1月至2018年12月全国民航客运量的时序图

16.5.2 FORECAST.ETS函数

  • FORECAST.ETS函数可以根据时间序列的历史数据识别长期趋势成分、季节变动。

  • 在实践中，需要注意的是，对于包含季节变动的序列，需要提供涵盖数个季节变动周期的历史数据，才能达到好的预测效果。

16.5.3 “预测工作表”工具

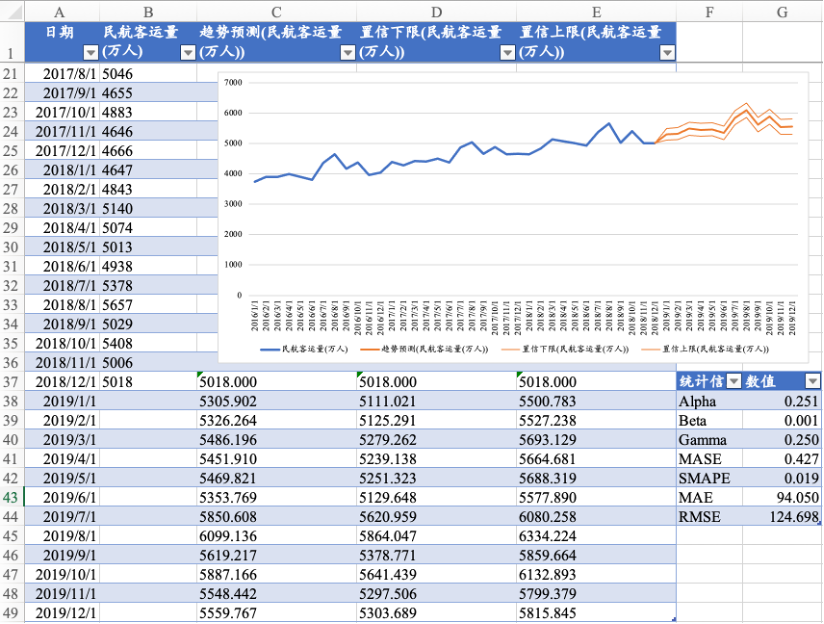
图16. 39 “预测工作表”工具的输出结果

第16章总结

https://lizongzhang.github.io/excelstat