第14章 相关分析

《精通Excel数据统计与分析》

2024-09-27

第14章 相关分析

• 14.1两个定性变量的关系

• 14.2两个定量变量的关系
  

14.1 两个定性变量的关系

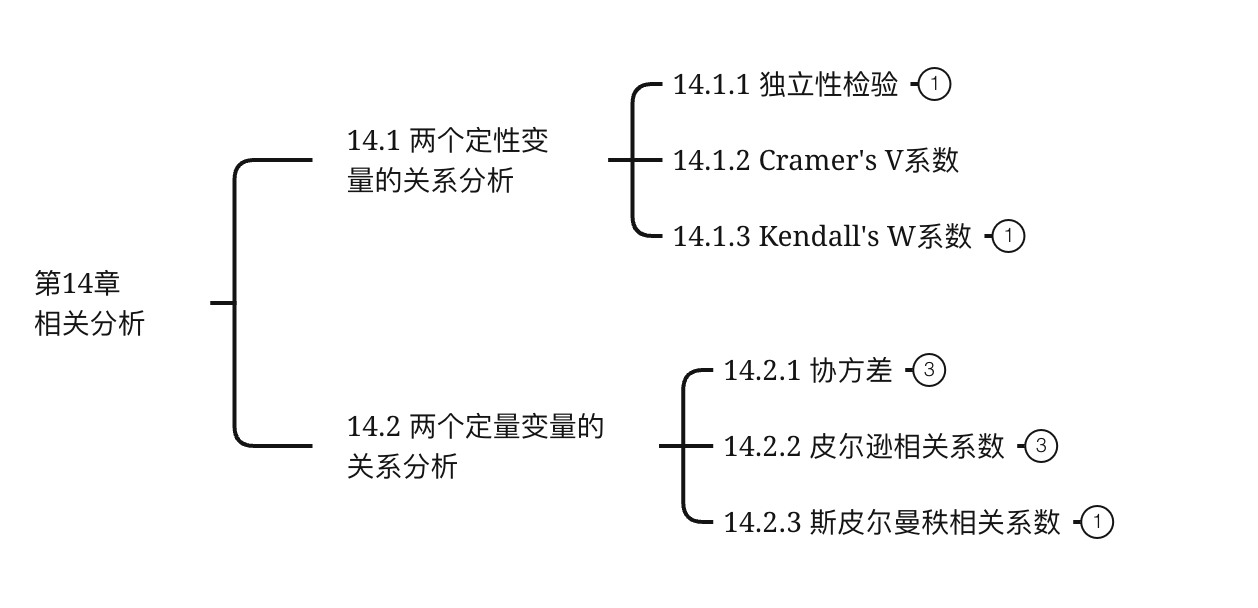
• 14.1.1 独立性检验

• 14.1.2 Cramer’s V系数

• 14.1.3 Kendall’s W系数

14.1.1 独立性检验

• 在独立性检验中，首先，在两个变量相互独立的假定下计算期望频数。

• 然后将观测频数与期望频数对比.

• 若二者差距较小，则说明两个变量相互独立；若二者差距很大，则说明两个变量不独立。

14.1.1 独立性检验

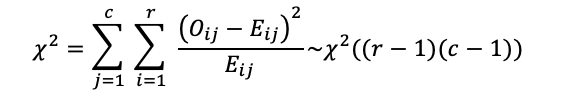
14.1.1 独立性检验

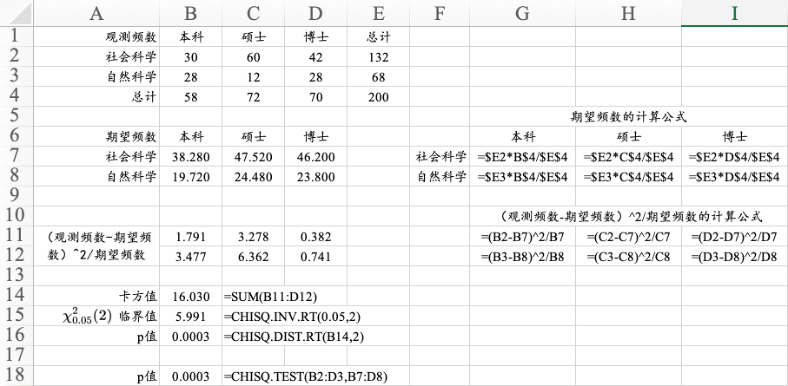
图14.1 独立性检验的计算过程

14.1.1 独立性检验

• 实操技巧

• 计算期望频数时只需录入左上角单元格的公式，恰当使用绝对引用符号$，然后拖曳单元格填充柄，实现自动计算。

• CHISQ.TEST函数可以计算独立性检验的p值，第1项参数是观测频数，第2项参数是期望频数。

• 若p值小于显著性水平∝，则拒绝“行变量和列变量相互独立”的原假设。

14.1.2 Cramer’s V系数

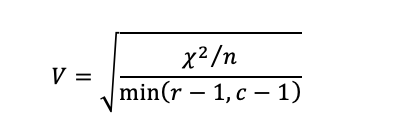
14.1.2 Cramer’s V系数

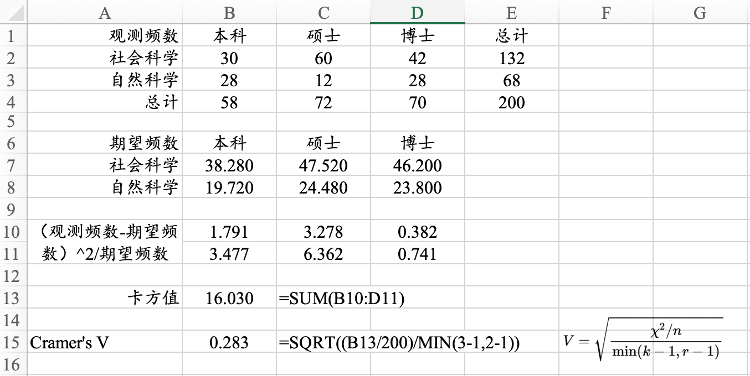
图14.3 Cramer’s V系数的计算过程

14.1.3 Kendall’s W系数

• Kendall’s W 系数又称作Kdendall一致系数（ Kendall’s Coefficient of Concordance），是一个非参数统计量，用于评估不同个体的主观态度或者评价是否一致。

• Kendall’s W系数的值介于0到1之间，等于0时代表态度完全不一致，等于0代表态度完全一致。

14.1.3 Kendall’s W系数

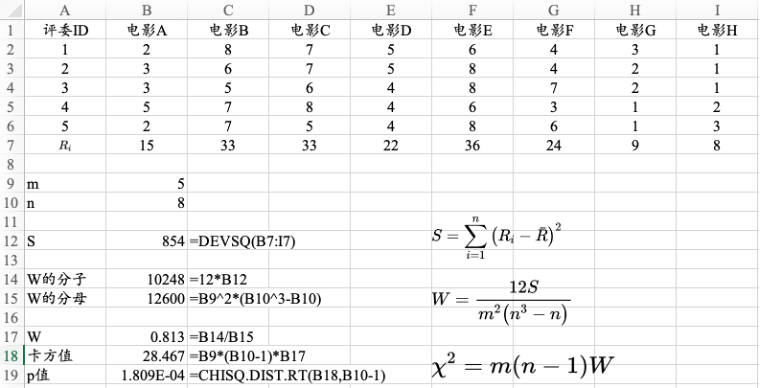
图14.4 Kendall’s W 系数的计算过程

14.1.3 Kendall’s W系数

• 实操技巧

• DEVSQ函数可以计算每个观测值与均值的离差平方和。

• 对Kendall’s W 系数进行显著性检验时，利用CHISQ.DIST.RT函数可以计算p值。若p值小于显著性水平，则拒绝“不同个体的主观评价是一致的”的原假设。

14.2两个定量变量的关系

• 14.2.1 协方差

• 14.2.2 皮尔逊相关系数

• 14.2.3 斯皮尔曼秩相关系数
  

14.2.1 协方差

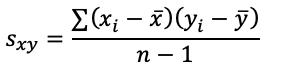
14.2.1 协方差

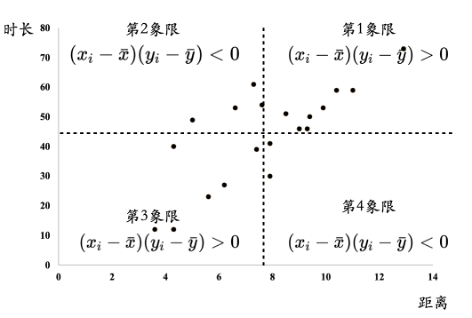
图14.7 协方差的符号的含义

14.2.2 皮尔逊相关系数

• 皮尔逊相关系数（Pearson Correlation Coefficient）也称作皮尔逊积矩相关系数（Pearson Product-moment Coefficient）

• 可以测度两个连续型定量变量之间的线性相关关系。

14.2.2 皮尔逊相关系数

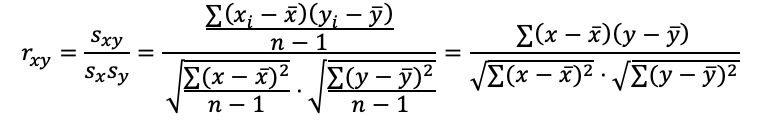
14.2.2 皮尔逊相关系数

• 实操技巧

• CORREL函数和PEARSON函数计算皮尔逊相关系数，第1项参数和第2项参数分别是两组数据区域，中间用逗号分隔。

• 单击“数据” →“数据分析” →“相关系数”，可以报告相关系数矩阵，矩阵对角线上的元素是1，非对角线上的元素是总体协方差。

14.2.3 斯皮尔曼秩相关系数

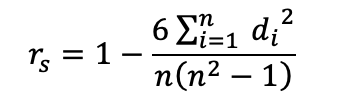
14.2.3 斯皮尔曼秩相关系数

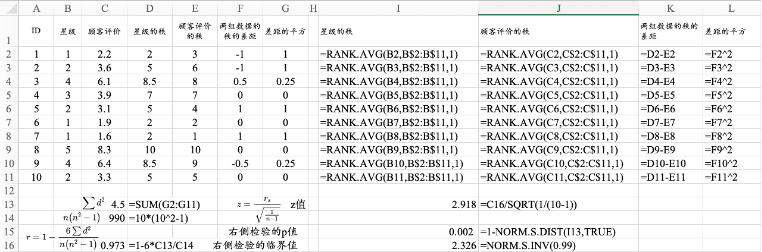
图14.13 斯皮尔曼秩相关系数的计算和检验

14.2.3 斯皮尔曼秩相关系数

• 实操技巧

• RANK.AVG函数可以计算观测值的秩。

第14章总结