第11章 两个总体参数的检验

《精通Excel数据统计与分析》

2024-09-27

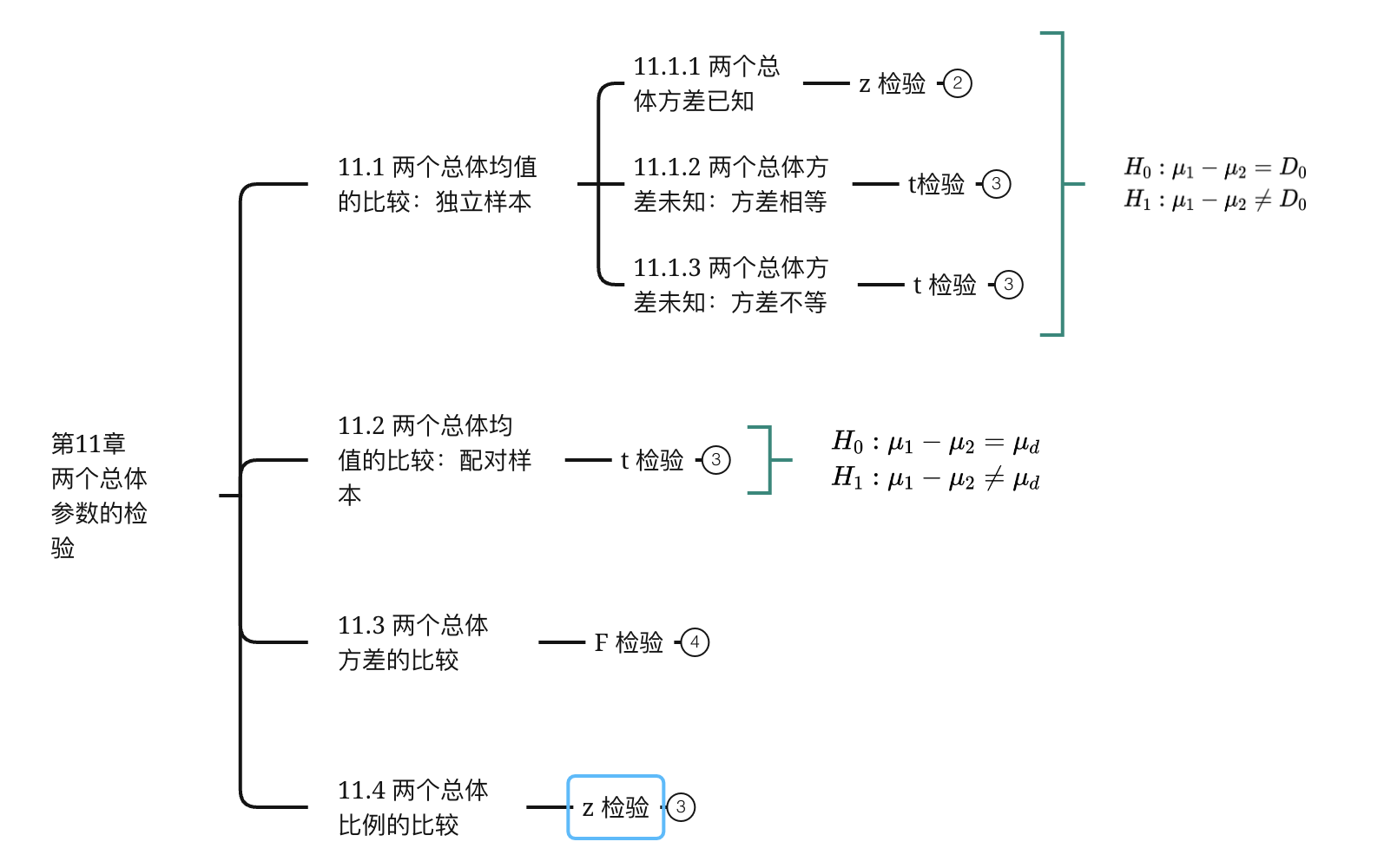
第11章 两个总体参数的检验

• 11.1 两个总体均值的比较：独立样本

• 两个总体的均值比较：配对样本

• 两个总体方差的比较

• 两个总体比例的比较

11.1 两个总体均值的比较：独立样本

• 11.1.1 两个总体方差已知：z检验

• 11.1.2 两个总体方差相等：t检验

• 11.1.3 两个总体方差不等：t检验

11.1.1 两个总体方差已知：z检验

11.1.1 两个总体方差已知：z检验

11.1.1 两个总体方差已知：z检验

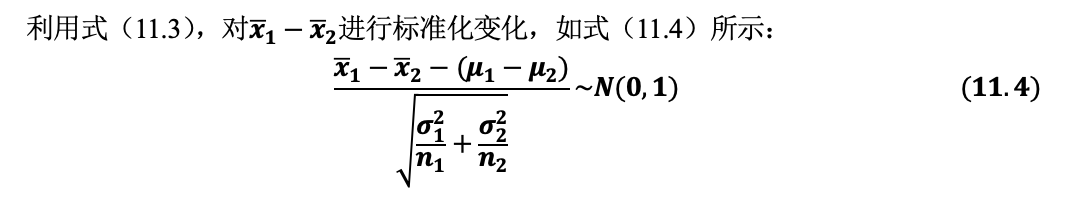
11.1.1 两个总体方差已知：z检验

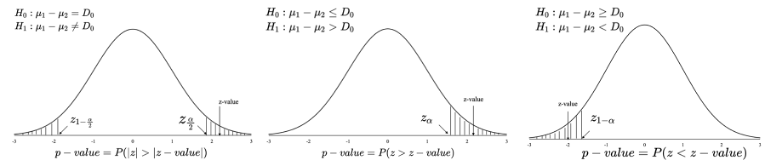
图11.1 z检验的临界值和拒绝域

11.1.1 两个总体方差已知：z检验

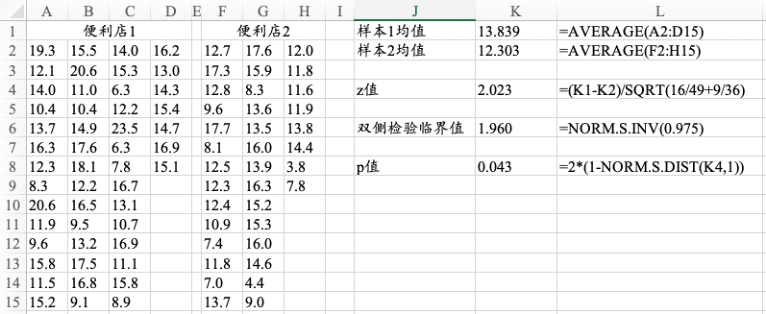
图11.2 两个总体方差已知的z检验的计算过程

11.1.1 两个总体方差已知：z检验

• Excel实操技巧

• 当两个总体标准差已知，比较两个总体均值的差异，可以调用“数据分析”工具下的“z检验：双样本平均差检验”，实现z检验的计算。

• 两个样本的数据需要排列在两行或者两列。

• 需要明确开展的是双侧检验还是单侧检验。双侧检验的p值报告在“P(Z<=z) 双尾”，单侧检验的p值报告在“P(Z<=z) 单尾”。

• 推荐使用p值法进行决策判断，若p值小于显著性水平α，则拒绝原假设；反之，则不拒绝原假设。

11.1.2 两个总体方差相等：t检验

11.1.2 两个总体方差相等：t检验

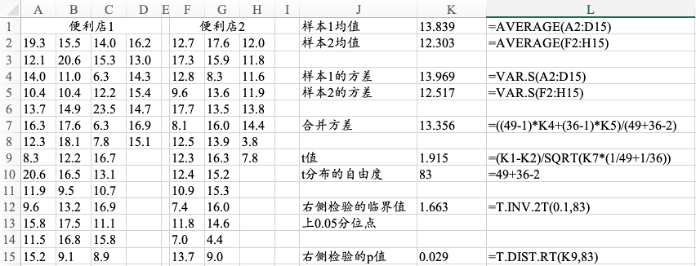
图11.7 两个总体方差相等的t检验的计算过程

11.1.2 两个总体方差相等：t检验

• Excel实操技巧

• 当两个总体的方差未知，假定两个总体的方差相等，若要比较两个总体的均值，可用“数据分析”工具中的 “t检验：双样本等方差假设” 实现t检验的计算。

11.1.3 两个总体方差不等：t检验

11.1.3 两个总体方差不等：t检验

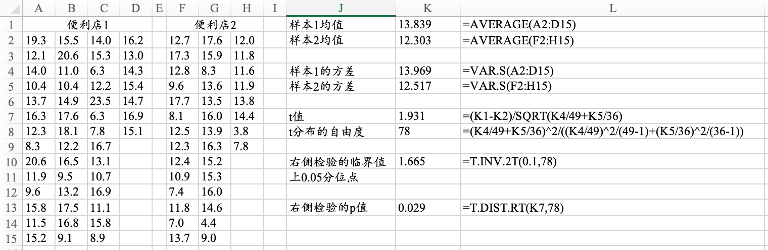
11.1.3 两个总体方差不等：t检验

• Excel实操技巧

• 当两个总体标准差未知，假定两个总体的方差不等，若要比较两个总体的均值，可用“数据分析”工具中的 “t检验：双样本异常方差假设”开展t检验。

11.2 两个总体的均值比较：配对样本

11.2 两个总体的均值比较：配对样本

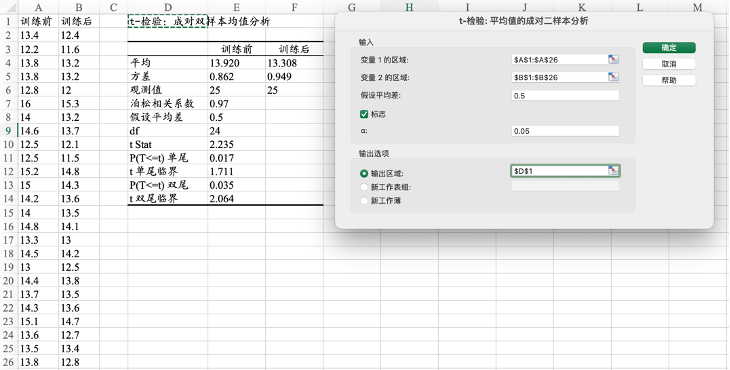
图11.12 “t检验：平均值的成对二样本分析”的对话框和输出结果

11.2 两个总体的均值比较：配对样本

• 实操技巧

• 若要比较两个配对总体的均值，可用“数据分析”工具中的 “t检验：平均值的成对二样本分析”实现t检验的计算。

11.3 两个总体方差的比较

11.3 两个总体方差的比较

图11.13 两个总体方差的F检验的计算过程

11.3 两个总体方差的比较

• 实操技巧

• 若要比较两个总体的方差，可用“数据分析”工具中的 “F检验：双样本方差”实现F检验的计算。

11.4 两个总体比例的比较

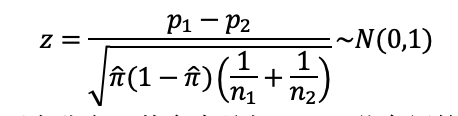
11.4 两个总体比例的比较

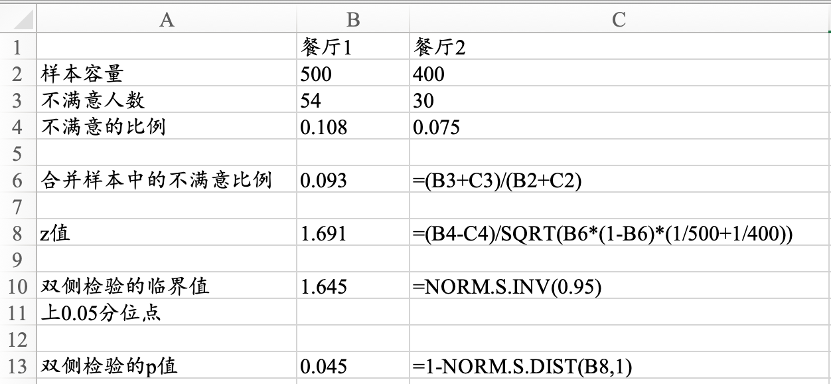
图11.15 两个总体比例的z检验的计算过程

11.4 两个总体比例的比较

• 实操技巧

• 先计算出样本比例，合并样本比例，然后编辑公式计算z值。

本章总结